题目内容
17. 将等腰Rt△ABC绕点A逆时针旋转15°得到△AB′C′,若AC=1,则图中阴影部分面积为( )
将等腰Rt△ABC绕点A逆时针旋转15°得到△AB′C′,若AC=1,则图中阴影部分面积为( )| A. | $\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{6}$ |
分析 设B′C′与AB交点为D,根据等腰直角三角形的性质求出∠BAC=45°,再根据旋转的性质求出∠CAC′=15°,AC′=AC,然后求出∠C′AD=30°,再根据直角三角形30°角所得到直角边等于斜边的一半可得AD=2C′D,然后利用勾股定理列式求出C′D,再利用三角形的面积公式列式进行计算即可得解.
解答 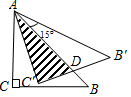 解:如图,设B′C′与AB交点为D,
解:如图,设B′C′与AB交点为D,
∵△ABC是等腰直角三角形,
∴∠BAC=45°,
∵△AB′C′是△ABC绕点A逆时针旋转15°后得到,
∴∠CAC′=15°,AC′=AC=1,
∴∠C′AD=∠BAC-∠CAC′=45°-15°=30°,
∵AD=2C′D,
∴AD2=AC′2+C′D2,
即(2C′D)2=12+C′D2,
解得C′D=$\frac{\sqrt{3}}{3}$,
故阴影部分的面积=$\frac{1}{2}$×1×$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{3}}{6}$.
故选D.
点评 本题考查了旋转的性质,等腰三角形的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,熟记性质并求出阴影部分的两直角边的长度是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
 某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )| A. | 该村人均耕地面积随总人口的增多而增多 | |
| B. | 当该村总人口为50人时,人均耕地面积为1公顷 | |
| C. | 若该村人均耕地面积为2公顷,则总人口有100人 | |
| D. | 该村人均耕地面积y与总人口x成正比例 |
12. 如图,在△ABC中,∠A=60°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )
如图,在△ABC中,∠A=60°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )
 如图,在△ABC中,∠A=60°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )
如图,在△ABC中,∠A=60°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )| A. | 105° | B. | 100° | C. | 95° | D. | 90° |
 在△ABC中,AD⊥BC于点D,BD=8,AD=6,S△ABC=42,那么AC的长为6$\sqrt{2}$.
在△ABC中,AD⊥BC于点D,BD=8,AD=6,S△ABC=42,那么AC的长为6$\sqrt{2}$. 如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和点B(b,0),交y轴于点C,抛物线的顶点为D.下列四个判断:
如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和点B(b,0),交y轴于点C,抛物线的顶点为D.下列四个判断: