题目内容
顺次连接一个四边形四边的中点得到的四边形是正方形，则原四边形是（ ）
| A、正方形 |
| B、矩形 |
| C、菱形 |
| D、对角线互相垂直且相等的四边形 |
考点：中点四边形
专题：
分析：由于顺次连接四边各边中点得到的四边形是平行四边形，由正方形的性质可知，原四边形应为对角线互相垂直且相等的四边形．
解答：解：由正方形的性质知，正方形的四角为直角，即每组邻边互相垂直且相等，
故原四边形的对角线互相垂直且相等的四边形．
故选：D．
故原四边形的对角线互相垂直且相等的四边形．
故选：D．
点评：本题考查的是正方形的判定定理以及中点四边形的性质，熟练掌握正方形的判定方法是解题关键．
练习册系列答案
相关题目
如图，已知△ABC三个内角的平分线交于点O，点D在CA的延长线上，且DC=BC，∠D=∠AOD，若∠BAC=80°，则∠BCA的度数为
直线AB：y=-x+b分别与x，y轴交于A（8、0）、B两点，过点B的直线交x轴轴负半轴于C，且OB：OC=4：3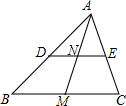
如图，△ABC中，AM是中线，点D、E分别在边AB、AC上，连接DE，且DE∥BC交AM于N，若DN=3，则DE=