题目内容
 如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,∠D=∠AOD,若∠BAC=80°,则∠BCA的度数为
如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,∠D=∠AOD,若∠BAC=80°,则∠BCA的度数为考点:全等三角形的判定与性质,等腰三角形的性质
专题:
分析:如图,证明∠D=20°;证明△BCO≌△DCO,得到∠OBC=∠D=20°,求出∠ABC,即可解决问题.
解答: 解:如图,∵△ABC三个内角的平分线交于点O,
解:如图,∵△ABC三个内角的平分线交于点O,
∴∠BAO=∠CAO,∠ABO=∠CBO;而∠BAC=80°,
∴∠OAC=40°;而∠D=∠AOD,
∴∠OAC=∠D+∠AOD=2∠D,
∴∠D=20°;
在△BCO与△DCO中,
,
∴△BCO≌△DCO(SAS),
∴∠OBC=∠D=20°,∠ABC=40°,
∴∠BCA=180°-80°-40°=60°,
故答案为60°.
 解:如图,∵△ABC三个内角的平分线交于点O,
解:如图,∵△ABC三个内角的平分线交于点O,∴∠BAO=∠CAO,∠ABO=∠CBO;而∠BAC=80°,
∴∠OAC=40°;而∠D=∠AOD,
∴∠OAC=∠D+∠AOD=2∠D,
∴∠D=20°;
在△BCO与△DCO中,
|
∴△BCO≌△DCO(SAS),
∴∠OBC=∠D=20°,∠ABC=40°,
∴∠BCA=180°-80°-40°=60°,
故答案为60°.
点评:该题主要考查了全等三角形的判定、三角形的内角和定理及其应用问题;解题的关键是牢固掌握全等三角形的判定等几何知识点.

练习册系列答案
相关题目
顺次连接一个四边形四边的中点得到的四边形是正方形,则原四边形是( )
| A、正方形 |
| B、矩形 |
| C、菱形 |
| D、对角线互相垂直且相等的四边形 |
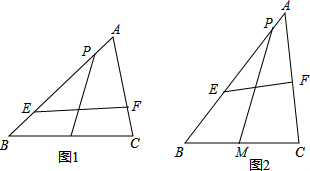
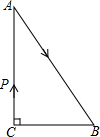 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒,问t为
如图,△ABC中,∠C=90°,AB=5cm,BC=3cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒,问t为