题目内容
某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
考点:二次函数的应用
专题:
分析:(1)先用待定系数法求出y与x之间的一次函数关系式,然后根据利润=销售量×(销售单价-成本)得到W与x之间的函数关系式;
(2)利用二次函数的性质,求出商场获得的最大利润以及获得最大利润时的售价.
(2)利用二次函数的性质,求出商场获得的最大利润以及获得最大利润时的售价.
解答:解:(1)根据题意得
,
解得
.
所求一次函数的表达式为y=-x+120.
(2)w=(x-60)(-x+120)
=-x2+180x-7200
=-(x-90)2+900,
∵抛物线的开口向下,
∴当x<90时,w随x的增大而增大,
而60≤x≤87,
∴当x=87时,w═-(87-90)2+900=891.
∴当销售单价定为87元时,商场可获得最大利润,最大利润是891元.
|
解得
|
所求一次函数的表达式为y=-x+120.
(2)w=(x-60)(-x+120)
=-x2+180x-7200
=-(x-90)2+900,
∵抛物线的开口向下,
∴当x<90时,w随x的增大而增大,
而60≤x≤87,
∴当x=87时,w═-(87-90)2+900=891.
∴当销售单价定为87元时,商场可获得最大利润,最大利润是891元.
点评:本题考查的是二次函数的应用,先用待定系数法求出销售量y(件)与销售单价x(元)之间的函数关系,然后求出利润W与x之间的二次函数,然后利用二次函数的性质以及题目中对销售单价的要求,求出最大利润和最大利润时的单价.

练习册系列答案
相关题目
顺次连接一个四边形四边的中点得到的四边形是正方形,则原四边形是( )
| A、正方形 |
| B、矩形 |
| C、菱形 |
| D、对角线互相垂直且相等的四边形 |
能说明△ABC≌△DEF的条件是( )
| A、AB=DE,AC=DF,∠C=∠F |
| B、AC=EF,∠A=∠D,∠B=∠E |
| C、AB=DE,BC=EF,∠A=∠D |
| D、BC=EF,AB=DE,∠B=∠E |
有6个大小、质地完全一样的球,2个红球,4个白球,装在盒子里搅匀,从中先后摸岀两个,摸岀后不放回.摸出的恰好是1个红球1个白球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
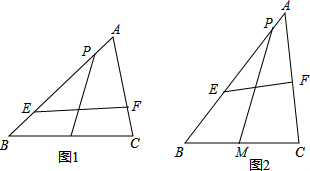
 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,联结DE,F为线段DE上一点,且∠AFE=∠B.若AB=5,AD=8,AE=4,则AF的长为
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,联结DE,F为线段DE上一点,且∠AFE=∠B.若AB=5,AD=8,AE=4,则AF的长为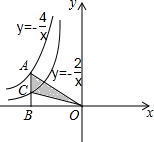 已知,如图,点A在反比例函数y=-
已知,如图,点A在反比例函数y=-