题目内容
计算:
(1)(x2-xy)÷
(2)
•
(3)
+
-
(4)
÷
•
.
(1)(x2-xy)÷
| y-x |
| xy |
(2)
| a2-4b2 |
| a2+2ab+b2 |
| a2+ab |
| a+2b |
(3)
| 2 |
| 3x2 |
| 3 |
| 4y |
| 5 |
| 6xy |
(4)
| x2-1 |
| (x-1)2 |
| 1 |
| x-1 |
| 1 |
| x+1 |
考点:分式的混合运算
专题:
分析:首先将所给分式分子、分母因式分解,然后化简、变形、约分、求值,即可解决问题.
解答:解:(1)原式
=x(x-y)×
=-x2y.
(2)原式
=
•
=
.
(3)
+
-
=
+
-
=
.
(4)
÷
•
=
×
×
=1.
=x(x-y)×
| xy |
| y-x |
=-x2y.
(2)原式
=
| (a+2b)(a-2b) |
| (a+b)2 |
| a(a+b) |
| a+2b |
=
| a2-2ab |
| a+b |
(3)
| 2 |
| 3x2 |
| 3 |
| 4y |
| 5 |
| 6xy |
=
| 8y2 |
| 12x2y2 |
| 9x2y |
| 12x2y2 |
| 10xy |
| 12x2y2 |
=
| 8y2+9x2y-10xy |
| 12x2y2 |
(4)
| x2-1 |
| (x-1)2 |
| 1 |
| x-1 |
| 1 |
| x+1 |
=
| (x+1)(x-1) |
| (x-1)2 |
| x-1 |
| 1 |
| 1 |
| x+1 |
=1.
点评:该题主要考查了分式的混合运算法则及其应用问题;解题的关键是准确运用因式分解法将所给的分式,分子、分母因式分解、恒等变形,然后化简求值.

练习册系列答案
相关题目
顺次连接一个四边形四边的中点得到的四边形是正方形,则原四边形是( )
| A、正方形 |
| B、矩形 |
| C、菱形 |
| D、对角线互相垂直且相等的四边形 |
有6个大小、质地完全一样的球,2个红球,4个白球,装在盒子里搅匀,从中先后摸岀两个,摸岀后不放回.摸出的恰好是1个红球1个白球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
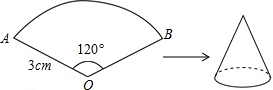 如图,已知扇形AOB的半径为3cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的侧面积为( )
如图,已知扇形AOB的半径为3cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的侧面积为( )| A、πcm2 |
| B、2πcm2 |
| C、3πcm2 |
| D、6πcm2 |
多项式x2-11x+30分解因式的结果为( )
| A、(x+5)(x-6) |
| B、(x-5)(x+6) |
| C、(x-5)(x-6) |
| D、(x+5)(x+6) |
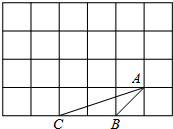 如图,在6×4的正方形方格中,△ABC的顶点A、B、C在单位正方形的格点上.
如图,在6×4的正方形方格中,△ABC的顶点A、B、C在单位正方形的格点上. 如图,正方形OABC中顶点B在一双曲线上,请在图中画出一条过点B的直线,使之与双曲线的另一支交于点D,且满足线段BD最短.
如图,正方形OABC中顶点B在一双曲线上,请在图中画出一条过点B的直线,使之与双曲线的另一支交于点D,且满足线段BD最短.