题目内容
计算:
(1)
+
+
-
-
.
(2)
+
-
(3)
÷
.
(1)
| a |
| a3+a2b+ab2+b3 |
| b |
| a3-a2b+ab2-b3 |
| 1 |
| a2-b2 |
| 1 |
| a2+b2 |
| a2+3b2 |
| a4-b4 |
(2)
| x3-1 |
| x3+2x2+2x+1 |
| x3+1 |
| x3-2x2+2x-1 |
| 2(x2+1) |
| x2-1 |
(3)
| ||||||||
|
| ||||
|
考点:分式的混合运算
专题:
分析:首先将所给的分式分子、分母因式分解,然后化简求值,即可解决问题.
解答:解:(1)原式=
+
+
-
-
=
+
=
-
=
-
=0.
(2)原式=
+
-
=
+
-
=
+
-
=
+
-
=
+
-
=
=0.
(3)原式=
÷
=
÷
=
×
=
=
.
| a |
| a2(a+b)+b2(a+b) |
| b |
| a2(a-b)+b2(a-b) |
| a2+b2 |
| a4-b4 |
| a2-b2 |
| a4-b4 |
| a2+3b2 |
| a4-b4 |
=
| a(a-b)+b(a+b) |
| (a+b)(a2+b2)(a-b) |
| -(a2+b2) |
| (a2+b2)(a2-b2) |
=
| a2+b2 |
| (a2+b2)(a2-b2) |
| 1 |
| a2-b2 |
=
| 1 |
| a2-b2 |
| 1 |
| a2-b2 |
=0.
(2)原式=
| x3-1 |
| x3+2x2+2x+1 |
| x3+1 |
| x3-2x2+2x-1 |
| 2(x2+1) |
| x2-1 |
=
| x3-1 |
| x2(x+1)+(x+1)2 |
| x3+1 |
| x2(x-1)-(x-1)2 |
| 2(x2+1) |
| x2-1 |
=
| (x-1)(x2+x+1) |
| (x+1)(x2+x+1) |
| (x+1)(x2-x+1) |
| (x-1)(x2-x+1) |
| 2x2+2 |
| x2-1 |
=
| x-1 |
| x+1 |
| x+1 |
| x-1 |
| 2x2+2 |
| x2-1 |
=
| (x-1)2 |
| x2-1 |
| (x+1)2 |
| x2-1 |
| 2x2+2 |
| x2-1 |
=
| x2-2x+1+x2+2x+1-2x2-2 |
| x2-1 |
=0.
(3)原式=
| ||||||||
|
| ||||
|
=
(
| ||||||||||||
(
|
| ||||
(
|
=
(
| ||||||||
(
|
(
| ||||
|
=
| ||||
|
=
| a2+b2 |
| b2-a2 |
点评:该题主要考查了分式的混合运算法则及其应用问题;解题的关键是准确运用因式分解法将所给的分式分子、分母因式分解,然后化简求值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
顺次连接一个四边形四边的中点得到的四边形是正方形,则原四边形是( )
| A、正方形 |
| B、矩形 |
| C、菱形 |
| D、对角线互相垂直且相等的四边形 |
能说明△ABC≌△DEF的条件是( )
| A、AB=DE,AC=DF,∠C=∠F |
| B、AC=EF,∠A=∠D,∠B=∠E |
| C、AB=DE,BC=EF,∠A=∠D |
| D、BC=EF,AB=DE,∠B=∠E |
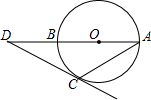 如图,AB是⊙O的直径,DC切⊙O于C,若∠A=25°,则∠D等于( )
如图,AB是⊙O的直径,DC切⊙O于C,若∠A=25°,则∠D等于( )| A、40° | B、50° |
| C、60° | D、70° |
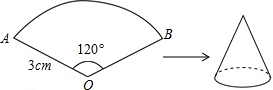 如图,已知扇形AOB的半径为3cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的侧面积为( )
如图,已知扇形AOB的半径为3cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的侧面积为( )| A、πcm2 |
| B、2πcm2 |
| C、3πcm2 |
| D、6πcm2 |
 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数y=
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数y=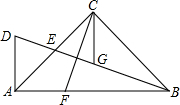 如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.求证:
如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.求证: