题目内容
 直线AB:y=-x+b分别与x,y轴交于A(8、0)、B两点,过点B的直线交x轴轴负半轴于C,且OB:OC=4:3
直线AB:y=-x+b分别与x,y轴交于A(8、0)、B两点,过点B的直线交x轴轴负半轴于C,且OB:OC=4:3(1)求点B的坐标为
(2)求直线BC的解析式;
(3)动点M从C出发沿CA方向运动,运动的速度为每秒1个单位长度.设M运动t秒时,当t为何值时△BCM为等腰三角形.
考点:一次函数综合题
专题:
分析:(1)根据待定系数法,可得AB的解析式,根据自变量的值,可得相应的函数值;
(2)根据OB:OC=4:3,可得OC的长,根据待定系数法,可得函数解析式;
(3)根据等腰三角形的定义,分类讨论:MC=BC,MC=MB,BC=BM,①当MC=BC时,根据路程处以速度等于时间,可得答案;②当MC=MB时,根据两点间的距离,可得关于a的方程,根据解方程,可得a的值,再根据路程除以速度等于时间,可得答案;③当BC=BM时,根据线段垂直平分线的性质,可得MO的长,再根据两点间的距离,可得MC的长,根据路程除以速度等于时间,可得答案.
(2)根据OB:OC=4:3,可得OC的长,根据待定系数法,可得函数解析式;
(3)根据等腰三角形的定义,分类讨论:MC=BC,MC=MB,BC=BM,①当MC=BC时,根据路程处以速度等于时间,可得答案;②当MC=MB时,根据两点间的距离,可得关于a的方程,根据解方程,可得a的值,再根据路程除以速度等于时间,可得答案;③当BC=BM时,根据线段垂直平分线的性质,可得MO的长,再根据两点间的距离,可得MC的长,根据路程除以速度等于时间,可得答案.
解答:解:(1)y=-x+b分别与x轴交于A(8、0),得
-8+b=0.解得b=8,
即函数解析式为y=-x+8,
当x=0时,y=8,
B点坐标是(0,8);
(2)由OB:OC=4:3,BC=8,得
8:BC=4:3,解得BC=6,即C(-6,0),
设直线BC的解析式为y=kx+b,图象经过点B,C,得
,解得
,
直线BC的解析式为y=
x+8;
(3)设M点坐标(a,0),由勾股定理,得BC=
=10,
①当MC=BC=10时,由路程处以速度等于时间,得10÷1=10(秒),
即M运动10秒,△BCM为等腰三角形;
②当MC=MB时,MC2=MB2,即(a+6)2=a2+82,
化简,得12a=28,
解得a=
即M(
,0).
MC=
-(-6)=
+6=
,
由路程除以速度等于时间,得
÷1=
(秒),
即M运动
秒时,△BCM为等腰三角形;
③当BC=BM时,得OC=OM=6,
即MC=6-(-6)=6+6=12,
由路程除以速度等于时间,得12÷1=12(秒),
即M运动12秒时,△BCM为等腰三角形,
综上所述:t=10(秒),t=
(秒),t=12(秒)时,△BCM为等腰三角形.
-8+b=0.解得b=8,
即函数解析式为y=-x+8,
当x=0时,y=8,
B点坐标是(0,8);
(2)由OB:OC=4:3,BC=8,得
8:BC=4:3,解得BC=6,即C(-6,0),
设直线BC的解析式为y=kx+b,图象经过点B,C,得
|
|
直线BC的解析式为y=
| 4 |
| 3 |
(3)设M点坐标(a,0),由勾股定理,得BC=
| OB2+OC2 |
①当MC=BC=10时,由路程处以速度等于时间,得10÷1=10(秒),
即M运动10秒,△BCM为等腰三角形;
②当MC=MB时,MC2=MB2,即(a+6)2=a2+82,
化简,得12a=28,
解得a=
| 7 |
| 3 |
| 7 |
| 3 |
MC=
| 7 |
| 3 |
| 7 |
| 3 |
| 25 |
| 3 |
由路程除以速度等于时间,得
| 25 |
| 3 |
| 25 |
| 3 |
即M运动
| 25 |
| 3 |
③当BC=BM时,得OC=OM=6,
即MC=6-(-6)=6+6=12,
由路程除以速度等于时间,得12÷1=12(秒),
即M运动12秒时,△BCM为等腰三角形,
综上所述:t=10(秒),t=
| 25 |
| 3 |
点评:本题考查了一次函数综合题,(1)利用待定系数法求函数解析式,自变量的值与函数值的对应关系;(2)利用待定系数求函数解析式;(3)利用等腰三角形的判定,分类讨论是解题关键.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
顺次连接一个四边形四边的中点得到的四边形是正方形,则原四边形是( )
| A、正方形 |
| B、矩形 |
| C、菱形 |
| D、对角线互相垂直且相等的四边形 |
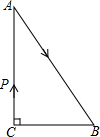 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒,问t为
如图,△ABC中,∠C=90°,AB=5cm,BC=3cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒,问t为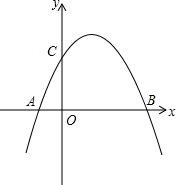 如图,抛物线y=
如图,抛物线y= 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数y=
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数y=