题目内容
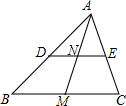 如图,△ABC中,AM是中线,点D、E分别在边AB、AC上,连接DE,且DE∥BC交AM于N,若DN=3,则DE=
如图,△ABC中,AM是中线,点D、E分别在边AB、AC上,连接DE,且DE∥BC交AM于N,若DN=3,则DE=考点:平行线分线段成比例,三角形中位线定理
专题:
分析:证明△ADN∽△ABN,得到
=
,
=
,进而得到
=
;证明BM=MC,得到NE=DN=3,即可解决问题.
| DN |
| BM |
| AN |
| AM |
| NE |
| MC |
| AN |
| AM |
| DN |
| BM |
| NE |
| MC |
解答: 解:∵DE∥BC,
解:∵DE∥BC,
∴△ADN∽△ABN,
∴
=
;
同理可证:
=
,
∴
=
;
∵AM是中线,
∴BM=MC,NE=DN=3,
故答案为6.
 解:∵DE∥BC,
解:∵DE∥BC,∴△ADN∽△ABN,
∴
| DN |
| BM |
| AN |
| AM |
同理可证:
| NE |
| MC |
| AN |
| AM |
∴
| DN |
| BM |
| NE |
| MC |
∵AM是中线,
∴BM=MC,NE=DN=3,
故答案为6.
点评:该题主要考查了平行线分线段成比例定理及其应用问题;牢固掌握定理的内容是灵活运用、解题的基础和关键.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
顺次连接一个四边形四边的中点得到的四边形是正方形,则原四边形是( )
| A、正方形 |
| B、矩形 |
| C、菱形 |
| D、对角线互相垂直且相等的四边形 |
能说明△ABC≌△DEF的条件是( )
| A、AB=DE,AC=DF,∠C=∠F |
| B、AC=EF,∠A=∠D,∠B=∠E |
| C、AB=DE,BC=EF,∠A=∠D |
| D、BC=EF,AB=DE,∠B=∠E |
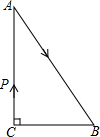 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒,问t为
如图,△ABC中,∠C=90°,AB=5cm,BC=3cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒,问t为 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数y=
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数y= 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,联结DE,F为线段DE上一点,且∠AFE=∠B.若AB=5,AD=8,AE=4,则AF的长为
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,联结DE,F为线段DE上一点,且∠AFE=∠B.若AB=5,AD=8,AE=4,则AF的长为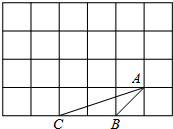 如图,在6×4的正方形方格中,△ABC的顶点A、B、C在单位正方形的格点上.
如图,在6×4的正方形方格中,△ABC的顶点A、B、C在单位正方形的格点上.