题目内容
13.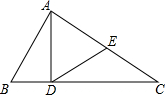 如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,DE为AC边上的中线,求证:∠BAD=∠EDC.
如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,DE为AC边上的中线,求证:∠BAD=∠EDC.
分析 根据直角三角形的两锐角互余即可证得∠BAD=∠C,然后利用直角三角形斜边上的中线等于斜边的一般证明△CDE是等腰三角形,利用等腰三角形的性质,以及等量代换即可证得.
解答 证明:∵∠BAC=90°,
∴∠BAD+∠DAC=90°,
又∵AD⊥BC,即∠ADC=90°,
∴∠DAC+∠C=90°,
∴∠BAD=∠C.
∵DE是直角△ACD斜边上的中线,
∴DE=$\frac{1}{2}$AC=EC,
∴∠C=∠EDC,
∴∠BAD=∠EDC.
点评 本题考查了直角三角形斜边上的中线等于斜边的一般,理解直角三角形被斜边上的中线分成两个等腰三角形是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4. 如图,2×5的正方形网格中,用5张1×2的矩形纸片将网格完全覆盖,则不同的覆盖方法有( )
如图,2×5的正方形网格中,用5张1×2的矩形纸片将网格完全覆盖,则不同的覆盖方法有( )
 如图,2×5的正方形网格中,用5张1×2的矩形纸片将网格完全覆盖,则不同的覆盖方法有( )
如图,2×5的正方形网格中,用5张1×2的矩形纸片将网格完全覆盖,则不同的覆盖方法有( )| A. | 3种 | B. | 5种 | C. | 8种 | D. | 13种 |
5. 已知:如图,在直角△ABC中,∠ACB=90°,∠CAB=30°,P为形内一点,∠BPC=120°,若BP=3,则△PAB的面积为( )
已知:如图,在直角△ABC中,∠ACB=90°,∠CAB=30°,P为形内一点,∠BPC=120°,若BP=3,则△PAB的面积为( )
 已知:如图,在直角△ABC中,∠ACB=90°,∠CAB=30°,P为形内一点,∠BPC=120°,若BP=3,则△PAB的面积为( )
已知:如图,在直角△ABC中,∠ACB=90°,∠CAB=30°,P为形内一点,∠BPC=120°,若BP=3,则△PAB的面积为( )| A. | 9 | B. | 4$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | $\frac{9\sqrt{3}}{2}$ |
2.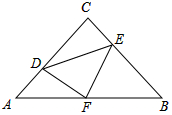 如图,在等腰Rt△ABC中,∠C=90°,AC=BC=4,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE,连接DE,DF,EF,在此运动变化过程中,则5个结论:①∠CDF=∠BEF;②△DFE是等腰直角三角形;③四边形CDFE的面积随D,E的运动而变化;④△CDE面积的最大值为4;⑤△DFE面积的最小值为2,其中正确的结论是( )
如图,在等腰Rt△ABC中,∠C=90°,AC=BC=4,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE,连接DE,DF,EF,在此运动变化过程中,则5个结论:①∠CDF=∠BEF;②△DFE是等腰直角三角形;③四边形CDFE的面积随D,E的运动而变化;④△CDE面积的最大值为4;⑤△DFE面积的最小值为2,其中正确的结论是( )
 如图,在等腰Rt△ABC中,∠C=90°,AC=BC=4,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE,连接DE,DF,EF,在此运动变化过程中,则5个结论:①∠CDF=∠BEF;②△DFE是等腰直角三角形;③四边形CDFE的面积随D,E的运动而变化;④△CDE面积的最大值为4;⑤△DFE面积的最小值为2,其中正确的结论是( )
如图,在等腰Rt△ABC中,∠C=90°,AC=BC=4,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE,连接DE,DF,EF,在此运动变化过程中,则5个结论:①∠CDF=∠BEF;②△DFE是等腰直角三角形;③四边形CDFE的面积随D,E的运动而变化;④△CDE面积的最大值为4;⑤△DFE面积的最小值为2,其中正确的结论是( )| A. | ①③⑤ | B. | ②③④ | C. | ①②⑤ | D. | ①②④ |
3.已知a、b是有理数,并且a2=$\frac{4}{9}$,|b|=$\frac{1}{3}$,如果a、b异号,那么a+b的值等于( )
| A. | 1 | B. | $\frac{1}{3}$ | C. | ±1 | D. | ±$\frac{1}{3}$ |
 如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的顶点处.
如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的顶点处. 如图,已知矩形ABCD中,AB=4,AD=3,P是以CD为直径的半圆上的一个动点,连接BP.
如图,已知矩形ABCD中,AB=4,AD=3,P是以CD为直径的半圆上的一个动点,连接BP.