题目内容
3.已知a、b是有理数,并且a2=$\frac{4}{9}$,|b|=$\frac{1}{3}$,如果a、b异号,那么a+b的值等于( )| A. | 1 | B. | $\frac{1}{3}$ | C. | ±1 | D. | ±$\frac{1}{3}$ |
分析 根据乘方的意义可得a=±$\frac{2}{3}$,根据绝对值的性质可得b=$±\frac{1}{3}$,再由条件a、b异号确定a、b的值,进而可得答案.
解答 解:∵a2=$\frac{4}{9}$,|b|=$\frac{1}{3}$,
∴a=±$\frac{2}{3}$,b=$±\frac{1}{3}$,
∵a、b异号,
∴①a=$\frac{2}{3}$,b=-$\frac{1}{3}$,则a+b=$\frac{1}{3}$,
②a=-$\frac{2}{3}$,b=$\frac{1}{3}$,则a+b=-$\frac{1}{3}$,
故选:D.
点评 此题主要考查了有理数的乘方和绝对值的性质,关键是掌握绝对值等于一个正数的数有两个,它们互为相反数;求n个相同因数积的运算,叫做乘方.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14. 如图,用三角尺可按下面方法画角平分线:在已知的∠AOB 的两边上分别取点M、N,使OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP.可证得△POM≌△PON,OP平分∠AOB.以上依画法证明△POM≌△PON根据的是( )
如图,用三角尺可按下面方法画角平分线:在已知的∠AOB 的两边上分别取点M、N,使OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP.可证得△POM≌△PON,OP平分∠AOB.以上依画法证明△POM≌△PON根据的是( )
 如图,用三角尺可按下面方法画角平分线:在已知的∠AOB 的两边上分别取点M、N,使OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP.可证得△POM≌△PON,OP平分∠AOB.以上依画法证明△POM≌△PON根据的是( )
如图,用三角尺可按下面方法画角平分线:在已知的∠AOB 的两边上分别取点M、N,使OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP.可证得△POM≌△PON,OP平分∠AOB.以上依画法证明△POM≌△PON根据的是( )| A. | SSS | B. | HL | C. | AAS | D. | SAS |
8.已知三角形三边长分别为5,x,17,若x为正整数,则这样的三角形个数为( )
| A. | 5个 | B. | 8个 | C. | 9个 | D. | 19个 |
13.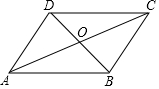 如图,已知AC、BD相交于点O,AO=CO,BO=DO,则图中能判定全等的三角形有( )
如图,已知AC、BD相交于点O,AO=CO,BO=DO,则图中能判定全等的三角形有( )
 如图,已知AC、BD相交于点O,AO=CO,BO=DO,则图中能判定全等的三角形有( )
如图,已知AC、BD相交于点O,AO=CO,BO=DO,则图中能判定全等的三角形有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
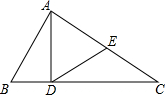 如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,DE为AC边上的中线,求证:∠BAD=∠EDC.
如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,DE为AC边上的中线,求证:∠BAD=∠EDC.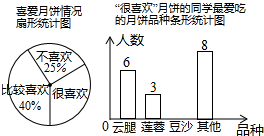 中秋佳节我国有赏月和吃月饼的传统,某校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了60名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图.(注:参与问卷调查的每一位同学在任何一种分类统计中只有一种选择)
中秋佳节我国有赏月和吃月饼的传统,某校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了60名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图.(注:参与问卷调查的每一位同学在任何一种分类统计中只有一种选择)