题目内容
2.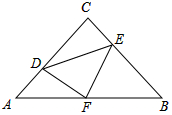 如图,在等腰Rt△ABC中,∠C=90°,AC=BC=4,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE,连接DE,DF,EF,在此运动变化过程中,则5个结论:①∠CDF=∠BEF;②△DFE是等腰直角三角形;③四边形CDFE的面积随D,E的运动而变化;④△CDE面积的最大值为4;⑤△DFE面积的最小值为2,其中正确的结论是( )
如图,在等腰Rt△ABC中,∠C=90°,AC=BC=4,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE,连接DE,DF,EF,在此运动变化过程中,则5个结论:①∠CDF=∠BEF;②△DFE是等腰直角三角形;③四边形CDFE的面积随D,E的运动而变化;④△CDE面积的最大值为4;⑤△DFE面积的最小值为2,其中正确的结论是( )| A. | ①③⑤ | B. | ②③④ | C. | ①②⑤ | D. | ①②④ |
分析 ①②正确,只要证明△CDF≌△BEF,即可证明.
③错误.根据四边形CDFE的面积=△CDF的面积+△CEF的面积=△BEF的面积+△CEF的面积=△BCF的面积=$\frac{1}{2}$△ABC的面积=定值,即可判断.
④错误.设AD=CE=x,则S△CDE=$\frac{1}{2}$(4-x)x=-$\frac{1}{2}$(x-2)2+2,利用二次函数的性质即可判断.
⑤正确.因为△DEF是等腰直角三角形,所以DE最小时,△DEF的面积最小,根据DE=$\sqrt{C{D}^{2}+C{E}^{2}}$=$\sqrt{(4-x)^{2}+{x}^{2}}$=$\sqrt{2(x-2)^{2}+8}$,利用二次函数的性质,即可判断.
解答 解:连接CF.
∵∠C=90°,AC=BC=4,F是AB边上的中点,
∴CF=AF=BF,∠DCF=∠B=45°,CF⊥AB,
∴∠CFB=90°,
∵AD=CE,
∴CD=BE,
在△CDF和△BEF中,
$\left\{\begin{array}{l}{CF=BF}\\{∠DCF=∠B}\\{CD=BE}\end{array}\right.$,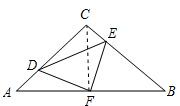
∴△CDF≌△BEF,
∴∠CDF=∠BEF,DE=EF,∠CFD=∠BFE,
∴∠DFE=∠CFB=90°,
∴△DEF是等腰直角三角形,故①②正确,
∵S△CDF=S△BFE,
∴四边形CDFE的面积=△CDF的面积+△CEF的面积=△BEF的面积+△CEF的面积=△BCF的面积=$\frac{1}{2}$△ABC的面积=定值,故③错误.
设AD=CE=x,
∴S△CDE=$\frac{1}{2}$(4-x)x=-$\frac{1}{2}$(x-2)2+2,
∵-$\frac{1}{2}$<0,
∴△CDE的面积的最大值为2,故④错误.
∵△DEF是等腰直角三角形,
∴DE最小时,△DEF的面积最小,
∵DE=$\sqrt{C{D}^{2}+C{E}^{2}}$=$\sqrt{(4-x)^{2}+{x}^{2}}$=$\sqrt{2(x-2)^{2}+8}$,
∴DE的最小值为2$\sqrt{2}$,此时DF=EF=2,
∴△DEF的面积的最小值=$\frac{1}{2}$×2×2=2,故⑤正确.
故选C.
点评 本题考查了等腰直角三角形的性质的运用,全等三角形的判定及性质的运用,三角形的面积公式的运用,勾股定理的运用,二次函数的解析式的性质的运用,解答时灵活运用等腰直角三角形的性质求解是关键.

 阅读快车系列答案
阅读快车系列答案| A. | 6 | B. | -2 | C. | 6或-2 | D. | 6或-1 |
| A. | a、b都是负数 | B. | b是正数,a是负数 | C. | a、b都是正数 | D. | a是正数,b是负数 |
| A. | 倒数 | B. | 相反数 | C. | 绝对值 | D. | 平方根 |
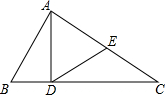 如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,DE为AC边上的中线,求证:∠BAD=∠EDC.
如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,DE为AC边上的中线,求证:∠BAD=∠EDC. 如图,用三角尺可按下面方法画角平分线:在已知的∠AOB 的两边上分别取点M、N,使OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP.可证得△POM≌△PON,OP平分∠AOB.以上依画法证明△POM≌△PON根据的是( )
如图,用三角尺可按下面方法画角平分线:在已知的∠AOB 的两边上分别取点M、N,使OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP.可证得△POM≌△PON,OP平分∠AOB.以上依画法证明△POM≌△PON根据的是( )