题目内容
9. 如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的顶点处.
如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的顶点处.(1)求AB的长;
(2)求点C到AB边距离.
分析 (1)直接利用勾股定理求出AB的长;
(2)利用△ABC的面积得出点C到AB边距离.
解答 解:(1)AB=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$;
(2)S△ABC=4×4-$\frac{1}{2}$×4×2-$\frac{1}{2}$×2×3-$\frac{1}{2}$×1×4=7,
设点C到AB边距离为h,则$\frac{1}{2}$×h×AB=7,
解得:h=$\frac{7}{\frac{1}{2}×2\sqrt{5}}$=$\frac{7\sqrt{5}}{5}$.
点评 此题主要考查了勾股定理以及三角形面积求法,正确利用勾股定理是解题关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
20. 如图,∠1=45°,∠3=105°,则∠2的度数为( )
如图,∠1=45°,∠3=105°,则∠2的度数为( )
 如图,∠1=45°,∠3=105°,则∠2的度数为( )
如图,∠1=45°,∠3=105°,则∠2的度数为( )| A. | 60° | B. | 55° | C. | 35° | D. | 30° |
17.已知∠A是锐角,且cosA=$\frac{\sqrt{3}}{2}$,那么∠A等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
 如图,AB是半圆O的直径,∠BAC=35°,则∠D的大小是125度.
如图,AB是半圆O的直径,∠BAC=35°,则∠D的大小是125度.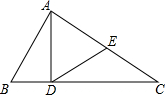 如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,DE为AC边上的中线,求证:∠BAD=∠EDC.
如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,DE为AC边上的中线,求证:∠BAD=∠EDC.