题目内容
如图，已知△ABC的六个元素，则下列甲、乙、丙三个三角形中和△ABC全等的图形是( )
A. 甲、乙 B. 甲、丙
C. 乙、丙 D. 甲、乙、丙
C
【解析】试题解析：由图形可知，甲有一边一角，不能判断两三角形全等，
乙有两边及其夹角，能判断两三角形全等，
丙得出两角及其一角对边，能判断两三角形全等，
根据全等三角形的判定得，乙丙正确.
故选C.
练习册系列答案
相关题目
如图所示，F、C在线段BE上，且∠1＝∠2，BC＝EF.若要根据“SAS”使△ABC≌△DEF，还需要补充的条件是________.
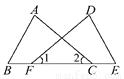
AC＝DF
【解析】已知∠1＝∠2，BC＝EF，根据“SAS”使△ABC≌△DEF，还需要补充的条件是AC＝DF. 小颖和小明做游戏:一个不透明的袋子中装有6个完全一样的球,每个球上分别标有1,2,2,3,4,5,从袋中任意摸出一个球,然后放回.规定:若摸到的球上所标数字大于3,则小颖赢,否则小明赢.你认为这个游戏公平吗?为什么?如果不公平,请修改游戏规则,使游戏公平.
游戏不公平.修改规则如下:方法一:若摸到的球上所标数字小于3,则小颖赢;否则小明赢.方法二:若摸到的球上所标数字是偶数,则小颖赢,否则小明赢.
【解析】试题分析：分别计算出小颖赢和小明赢的概率即可；通过比较概率的大小来判断游戏是否公平．
试题解析：【解析】
P（小颖赢）=，P（小明赢）=，所以不公平．
修改规则如下：方法一：若摸到的球上所标数字小于3，则小颖赢；否则小明赢．
... 如图，A、B、C分别是线段A1B、B1C、C1A的中点，若△ABC的面积是1，那么△A1B1C1的面积为____.
7
【解析】试题分析：如下图，连接A1C，B1A，C1B，，因B是线段B1C的中点，所以B1B="BC." △A1B1A和△AB1B等底同高，根据等底同高的两个三角形面积相等可得S△B1AB=S△ABC=1；同理可得S△A1B1A=S△AB1B=1；所以=S△A1B1A+S△AB1B=1+1=2；同理可得S△C1CB1=2， S△C1AA1=2.
S△A1B1C1= S△A1BB1+ ... 如图所示，在△ABC中，AQ=PQ，PR=PS，PR⊥AB于R，PS⊥AC于S，则下列三个结论：①AS=AR；②QP∥AR；③△BPR≌△QPS中（ ）
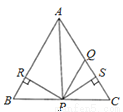
A. 全部正确 B. 仅①和②正确 C. 仅①正确 D. 仅①和③正确
B
【解析】∵PR=PS，PR⊥AB于R，PS⊥AC于S，
∴∠PAB=∠PAC，∠PSA=∠PRA=90°，
在△PAR和△PAS中，
，
∴△PAR≌△PAS（AAS），
∴AR=AS，∴①正确；
∵AQ=PQ，
∠CAP=∠APQ，
∵∠CAP=∠BAP，
∴∠BAP=∠APQ，
∴PQ∥AB，∴②正确；
∵PR⊥AB，... 一堆有红、白两种颜色的球若干个，已知白球的个数比红球少，但白球的2倍比红球多．若把每一个白球都记作“2”，每一个红球都记作“3”，则总数为“60”，那么这两种球各有多少个？
白球有9个，红球有14个．
【解析】【试题分析】设白球有x个，红球有y个，根据“白球的个数比红球少，但白球的2倍比红球多”，得 ，解得7.5＜x＜12，则x可以取8,9,10,11.
由于2x=60－3y=3（20－y） 得2x应是3的倍数，则x只能取9，y = = 14
即白球有9个，红球有14个．
【试题解析】
设白球有x个，红球有y个，由题意，得
由第一个... －3x≤6的解集是 （ ）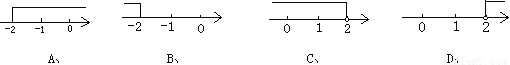
A
【解析】试题分析：由－3x≤6解得x≥－2，即可得到结果.
－3x≤6解得x≥－2，故选A. 已知一副直角三角板如图放置，其中BC＝3，EF＝4，把30°的三角板向右平移，使顶点B落在45°的三角板的斜边DF上，则AE＝ _________.
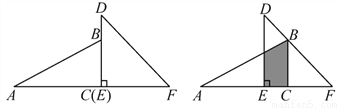
3－1
【解析】试题分析：∵∠F＝45°，BC＝3，
∴CF＝3，又EF＝4，
则EC＝1，
∵BC＝3，∠A＝30°，
∴AC＝，
则AE＝－1．
故答案为： －1．