题目内容
已知一副直角三角板如图放置，其中BC＝3，EF＝4，把30°的三角板向右平移，使顶点B落在45°的三角板的斜边DF上，则AE＝ _________.
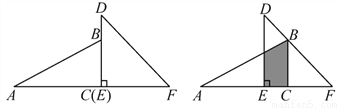
3－1
【解析】试题分析：∵∠F＝45°，BC＝3，
∴CF＝3，又EF＝4，
则EC＝1，
∵BC＝3，∠A＝30°，
∴AC＝，
则AE＝－1．
故答案为： －1．
练习册系列答案
相关题目
如图，已知△ABC的六个元素，则下列甲、乙、丙三个三角形中和△ABC全等的图形是( )
A. 甲、乙 B. 甲、丙
C. 乙、丙 D. 甲、乙、丙
C
【解析】试题解析：由图形可知，甲有一边一角，不能判断两三角形全等，
乙有两边及其夹角，能判断两三角形全等，
丙得出两角及其一角对边，能判断两三角形全等，
根据全等三角形的判定得，乙丙正确.
故选C. 利用尺规作三角形,有三种基本类型:
(1)已知三角形的两边及其夹角,求作符合要求的三角形,其作图依据是“____”;
(2)已知三角形的两角及其夹边,求作符合要求的三角形,其作图依据是“____”;
(3)已知三角形的三边,求作符合要求的三角形,其作图依据是“____”.
SAS ASA SSS
【解析】根据SAS—两边及其夹角分别相等的两个三角形全等；ASA—两角及其夹边分别相等的两个三角形全等；SSS—三边分别相等的两个三角形全等.
故答案：(1)SAS、 (2)ASA 、(3)SSS. 如图所示，AB与CD相交所成的四个角中，∠1的邻补角是__________，∠1的对顶角是__________.
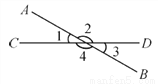
∠2，∠4 ∠3
【解析】根据对顶角和邻补角的定义解答，注意两直线相交，一个角的对顶角只有一个，但邻补角有两个．
【解析】
由图形可知，∠1的对顶角是∠3，
∠1的邻补角是∠2和∠4． 如图（1）将△ABD平移，使D沿BD延长线移至C得到△A′B′D′，A′B′交AC于E，AD平分∠BAC．
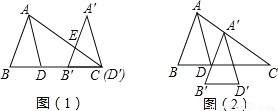
（1）猜想∠B′EC与∠A′之间的关系，并写出理由．
（2）如图将△ABD平移至如图（2）所示，得到△A′B′D′，请问：A′D平分∠B′A′C吗？为什么？
（1）∠B′EC=2∠A′；（2）A′D′平分∠B′A′C．见解析
【解析】
试题分析：（1）根据平移的性质得出∠BAD=∠DAC，∠BAD=∠A′，AB∥A′B′，进而得出∠BAC=∠B′EC，进而得出答案；
（2）利用平移的性质得出∠B′A′D′=∠BAD，AB∥A′B′，进而得出∠BAD=∠BAC，即可得出∠B′A′D′=∠B′A′C．
【解析】
（1）∠B′EC=... 在图示的四个汽车标志图案中，能用平移变换来分析其形成过程的图案是( )
A. 
B. 
C. 
D. 
D
【解析】试题分析：根据平移的概念，即平移前后图形的大小，形状都不变，只是位置改变.
故选D. 已知tanβ=22.3，则β=_________（精确到1″）
87°25′56″
【解析】试题分析：利用计算器首先按2ndF，再按tan，再输入22.3，再按DMS即可得出答案．
∵tanβ=22.3，∴β=87°25′56″．
故答案为：87°25′56″ 下面四个数中，最大的是（ ）
A.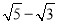 
B. sin88° C. tan46° D.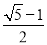 
C
【解析】试题分析：A、≈2.236-1.732≈0.504；
B、sin88°≈0.999；
C、tan46°≈1.036；
D、 ≈ ≈0.568．
故tan46°最大，
故选：C． 若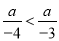
，试判断a的正负性．
a为负数
【解析】分析：先根据不等式基本性质3,两边都乘以,再根据不等式基本性质1,两边都减去3a即可得出结论.
本题解析：根据不等式基本性质3，两边都乘以－12，得3a＞4a．
根据不等式基本性质1，两边都减去3a，得0＞a ，即a<0 ，即a为负数．