题目内容
小颖和小明做游戏:一个不透明的袋子中装有6个完全一样的球,每个球上分别标有1,2,2,3,4,5,从袋中任意摸出一个球,然后放回.规定:若摸到的球上所标数字大于3,则小颖赢,否则小明赢.你认为这个游戏公平吗?为什么?如果不公平,请修改游戏规则,使游戏公平.
 游戏不公平.修改规则如下:方法一:若摸到的球上所标数字小于3,则小颖赢;否则小明赢.方法二:若摸到的球上所标数字是偶数,则小颖赢,否则小明赢.
【解析】试题分析:分别计算出小颖赢和小明赢的概率即可;通过比较概率的大小来判断游戏是否公平.
试题解析:【解析】
P(小颖赢)=,P(小明赢)=,所以不公平.
修改规则如下:方法一:若摸到的球上所标数字小于3,则小颖赢;否则小明赢.
...
游戏不公平.修改规则如下:方法一:若摸到的球上所标数字小于3,则小颖赢;否则小明赢.方法二:若摸到的球上所标数字是偶数,则小颖赢,否则小明赢.
【解析】试题分析:分别计算出小颖赢和小明赢的概率即可;通过比较概率的大小来判断游戏是否公平.
试题解析:【解析】
P(小颖赢)=,P(小明赢)=,所以不公平.
修改规则如下:方法一:若摸到的球上所标数字小于3,则小颖赢;否则小明赢.
...
用直尺和圆规作一个角的平分线如图所示,说明∠AOC=∠BOC的依据是( ).
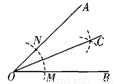
A. SSS B. ASA C. AAS D. 角平分线上的点到角两边距离相等
 A
【解析】试题分析:连接NC,MC,根据SSS证△ONC≌△OMC,即可推出答案.
连接NC,MC,在△ONC和△OMC中,
∴△ONC≌△OMC(SSS), ∴∠AOC=∠BOC
A
【解析】试题分析:连接NC,MC,根据SSS证△ONC≌△OMC,即可推出答案.
连接NC,MC,在△ONC和△OMC中,
∴△ONC≌△OMC(SSS), ∴∠AOC=∠BOC 如图,巳知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于B,连AB,∠α=75°,则b值为( )
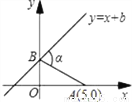
A. 3 B.  C. 4 D.
C. 4 D. 
 B
【解析】因为直线的解析式是y=x+b,
∴OB=OC=b,则∠BCA=45°;
又∵∠α=75°=∠BCA+∠BAC=45°+∠BAC(外角定理)
∴∠BAC=30°;
而点A的坐标是(5,0),
∴OA=5,
在Rt△BAO中,∠BAC=30°,OA=5,
∴tan∠BAO=
∴BO=,即b=.
故选B.
B
【解析】因为直线的解析式是y=x+b,
∴OB=OC=b,则∠BCA=45°;
又∵∠α=75°=∠BCA+∠BAC=45°+∠BAC(外角定理)
∴∠BAC=30°;
而点A的坐标是(5,0),
∴OA=5,
在Rt△BAO中,∠BAC=30°,OA=5,
∴tan∠BAO=
∴BO=,即b=.
故选B. 如图所示,转盘被等分成六个扇形,并在上面依次写上数字1、2、3、4、5、6.
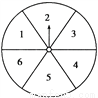
(1)若自由转动转盘,当它停止转动时,指针指向奇数区的概率是多少?
(2)请你用这个转盘设计一个游戏,当自由转动的转盘停止时,指针指向的区域的概率为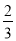 .
.
 (1);(2)详见解析.
【解析】试题分析:(1)自由转动转盘,当它停止转动时,指针指向数字的结果总共有6种,指针指向奇数区的结果有3种,所以指针指向奇数区的概率是.
(2)当自由转动的转盘停止时,指针指向的区域不大于4.(答案不唯一,符合要求即可)
试题解析:(1)指针指向奇数区的概率是.
(2)当自由转动的转盘停止时,指针指向的区域不大于4.(答案不唯一,符合要求即可)...
(1);(2)详见解析.
【解析】试题分析:(1)自由转动转盘,当它停止转动时,指针指向数字的结果总共有6种,指针指向奇数区的结果有3种,所以指针指向奇数区的概率是.
(2)当自由转动的转盘停止时,指针指向的区域不大于4.(答案不唯一,符合要求即可)
试题解析:(1)指针指向奇数区的概率是.
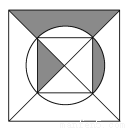
(2)当自由转动的转盘停止时,指针指向的区域不大于4.(答案不唯一,符合要求即可)... 在如图所示的正方形纸片上做随机扎针实验,则针头扎在阴影区域内的概率为( )
A.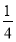 B.
B.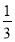
C.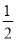 D.
D.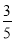
 A
【解析】根据正方形的性质易证正方形的对角线把正方形分成的四个三角形均为同底等高的三角形,故其面积相等,故阴影部分的面积占一份,故针头扎在阴影区域的概率为.
A
【解析】根据正方形的性质易证正方形的对角线把正方形分成的四个三角形均为同底等高的三角形,故其面积相等,故阴影部分的面积占一份,故针头扎在阴影区域的概率为. 某口袋中有20个球,每个球除颜色外都相同,其中白球x个,绿球2x个,其余为黑球,甲从袋中任意摸出一个球,若为绿球则获胜,甲摸出的球放回袋中,乙从袋中摸出一个球,若为黑球则获胜.若对甲、乙双方公平,则x等于( )
A. 3 B. 4 C. 5 D. 6
 B
【解析】【解析】
根据题意得: ,即2x=20-x-2x,解得:x=4.故选B.
B
【解析】【解析】
根据题意得: ,即2x=20-x-2x,解得:x=4.故选B. 如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:∠B=∠E.

 证明见解析.
【解析】试题分析:根据AB//CD得出∠DCA=∠CAB,结合AB=CE,AC=CD得出△CAB≌△DCE,从而得出答案.
试题解析:∵AB//CD,∴∠DCA=∠CAB 又∵AB=CE,AC=CD,∴△CAB≌△DCE ∴∠B=∠E.
证明见解析.
【解析】试题分析:根据AB//CD得出∠DCA=∠CAB,结合AB=CE,AC=CD得出△CAB≌△DCE,从而得出答案.
试题解析:∵AB//CD,∴∠DCA=∠CAB 又∵AB=CE,AC=CD,∴△CAB≌△DCE ∴∠B=∠E. 如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中和△ABC全等的图形是( )

A. 甲、乙 B. 甲、丙
C. 乙、丙 D. 甲、乙、丙
 C
【解析】试题解析:由图形可知,甲有一边一角,不能判断两三角形全等,
乙有两边及其夹角,能判断两三角形全等,
丙得出两角及其一角对边,能判断两三角形全等,
根据全等三角形的判定得,乙丙正确.
故选C.
C
【解析】试题解析:由图形可知,甲有一边一角,不能判断两三角形全等,
乙有两边及其夹角,能判断两三角形全等,
丙得出两角及其一角对边,能判断两三角形全等,
根据全等三角形的判定得,乙丙正确.
故选C. 利用尺规作三角形,有三种基本类型:
(1)已知三角形的两边及其夹角,求作符合要求的三角形,其作图依据是“____”;
(2)已知三角形的两角及其夹边,求作符合要求的三角形,其作图依据是“____”;
(3)已知三角形的三边,求作符合要求的三角形,其作图依据是“____”.
 SAS ASA SSS
【解析】根据SAS—两边及其夹角分别相等的两个三角形全等;ASA—两角及其夹边分别相等的两个三角形全等;SSS—三边分别相等的两个三角形全等.
故答案:(1)SAS、 (2)ASA 、(3)SSS.
SAS ASA SSS
【解析】根据SAS—两边及其夹角分别相等的两个三角形全等;ASA—两角及其夹边分别相等的两个三角形全等;SSS—三边分别相等的两个三角形全等.
故答案:(1)SAS、 (2)ASA 、(3)SSS. 
