题目内容
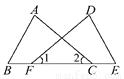
如图所示，F、C在线段BE上，且∠1＝∠2，BC＝EF.若要根据“SAS”使△ABC≌△DEF，还需要补充的条件是________.
AC＝DF
【解析】已知∠1＝∠2，BC＝EF，根据“SAS”使△ABC≌△DEF，还需要补充的条件是AC＝DF.
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
在Rt△ABC中，∠C＝90°，BC＝3，AC＝4，那么cos A的值等于 ．
．
【解析】
试题分析：∵在Rt△ABC中，∠C=90°，AC=4，BC=3，∴AB==，∴cosA==，故答案为：． 用直尺和圆规作一个角的平分线如图所示，说明∠AOC＝∠BOC的依据是( )．
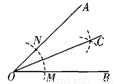
A. SSS B. ASA C. AAS D. 角平分线上的点到角两边距离相等
A
【解析】试题分析：连接NC，MC，根据SSS证△ONC≌△OMC，即可推出答案．
连接NC，MC，在△ONC和△OMC中，
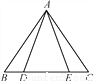
∴△ONC≌△OMC（SSS）， ∴∠AOC=∠BOC 如图，点D，E在△ABC的边BC上，AB＝AC，BD＝CE.
求证：AD＝AE.
证明见解析
【解析】试题分析：利用等腰三角形的性质得到∠B=∠C，然后证明△ABD≌△ACE即可证得结论．
【解答】证明：∵AB=AC，
∴∠B=∠C，
在△ABD与△ACE中，
∵，
∴△ABD≌△ACE（SAS），
∴AD=AE． 如图，AB∥CE，BF交CE于点D，DE＝DF，∠F＝20°，则∠B的度数为______．
40度
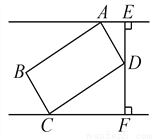
【解析】试题分析：由题可知，DE＝DF，∠F＝20°∴∠E=∠F＝20°∴∠BDE=∠E+∠F=40°，又 AB∥CE，∴∠B=∠BDE=40°，故答案为40度。 如图，矩形ABCD是供一机动车停放的车位示意图，已知BC＝2m，CD＝5.4m，∠DCF＝30°.请你计算车位所占的宽度EF约为多少米？(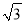
≈1.73，结果保留一位小数)
4.4米
【解析】试题分析：分别在Rt△BCF和Rt△AEF中求得DF和DE的长后，相加即可得到EF的长．
试题解析：
在Rt△DCF中，
∵CD=5.4m，∠DCF=30°，
∴sin∠DCF=，
∴DF=2.7m，
∵∠CDF+∠DCF=90°∠ADE+∠CDF=90°，
∴∠ADE=∠DCF=30°，
∵AD=BC=2，
∴cos∠... 如图,巳知A点坐标为(5,0),直线y=x+b(b＞0)与y轴交于B,连AB,∠α=75°,则b值为（ ）
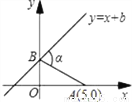
A. 3 B. 
C. 4 D. 
B
【解析】因为直线的解析式是y=x+b，
∴OB=OC=b,则∠BCA=45°；
又∵∠α=75°=∠BCA+∠BAC=45°+∠BAC(外角定理)
∴∠BAC=30°；
而点A的坐标是(5,0)，
∴OA=5，
在Rt△BAO中,∠BAC=30°，OA=5，
∴tan∠BAO=
∴BO=,即b=.
故选B. 如图所示，转盘被等分成六个扇形，并在上面依次写上数字1、2、3、4、5、6.
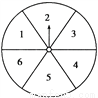
（1）若自由转动转盘，当它停止转动时，指针指向奇数区的概率是多少？
（2）请你用这个转盘设计一个游戏，当自由转动的转盘停止时，指针指向的区域的概率为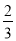
.
（1）；（2）详见解析．
【解析】试题分析：（1）自由转动转盘，当它停止转动时，指针指向数字的结果总共有6种，指针指向奇数区的结果有3种，所以指针指向奇数区的概率是．
（2）当自由转动的转盘停止时，指针指向的区域不大于4．（答案不唯一，符合要求即可）
试题解析：（1）指针指向奇数区的概率是．
（2）当自由转动的转盘停止时，指针指向的区域不大于4．（答案不唯一，符合要求即可）... 如图，已知△ABC的六个元素，则下列甲、乙、丙三个三角形中和△ABC全等的图形是( )
A. 甲、乙 B. 甲、丙
C. 乙、丙 D. 甲、乙、丙
C
【解析】试题解析：由图形可知，甲有一边一角，不能判断两三角形全等，
乙有两边及其夹角，能判断两三角形全等，
丙得出两角及其一角对边，能判断两三角形全等，
根据全等三角形的判定得，乙丙正确.
故选C.