练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
如图,巳知A点坐标为(5,0),直线y=x+b(b＞0)与y轴交于B,连AB,∠α=75°,则b值为（ ）
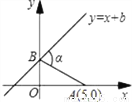
A. 3 B. 
C. 4 D. 
B
【解析】因为直线的解析式是y=x+b，
∴OB=OC=b,则∠BCA=45°；
又∵∠α=75°=∠BCA+∠BAC=45°+∠BAC(外角定理)
∴∠BAC=30°；
而点A的坐标是(5,0)，
∴OA=5，
在Rt△BAO中,∠BAC=30°，OA=5，
∴tan∠BAO=
∴BO=,即b=.
故选B. 如图，在△ABC和△CED中，AB∥CD，AB=CE，AC=CD.求证：∠B=∠E.
证明见解析.
【解析】试题分析：根据AB//CD得出∠DCA=∠CAB，结合AB=CE，AC=CD得出△CAB≌△DCE，从而得出答案.
试题解析：∵AB//CD，∴∠DCA=∠CAB 又∵AB=CE，AC=CD，∴△CAB≌△DCE ∴∠B=∠E. 如图，已知△ABC的六个元素，则下列甲、乙、丙三个三角形中和△ABC全等的图形是( )
A. 甲、乙 B. 甲、丙
C. 乙、丙 D. 甲、乙、丙
C
【解析】试题解析：由图形可知，甲有一边一角，不能判断两三角形全等，
乙有两边及其夹角，能判断两三角形全等，
丙得出两角及其一角对边，能判断两三角形全等，
根据全等三角形的判定得，乙丙正确.
故选C. |2a－24|＋（3a－b－k）2＝0，那么k取什么值时，b为负数．
k大于36时b为负数．
【解析】【试题分析】根据绝对值和完全平方的非负性，得 解得：a=12，b=36-k,当b<0时，即36-k<0，解得k>36.
【试题解析】
由题意得： 解得：b=36-k,
解得k>36.
故答案为k>36. 不等式－2x＜8的负整数解的和是______．
－6
【解析】解不等式－2x＜8 得： ，则它的负整数解为x=-1,-2,-3,故原不等式的负整数解的和为 .故答案为-6. 不等式2x＜6的非负整数解为( )
A.0，1，2 B.1，2 C.0，－1，－2 D.无数个
A
【解析】
试题分析：先根据不等式的基本性质求得不等式的解集，即可得到结果.
由2x＜6得x＜3，非负整数解为0，1，2
故选A. 利用尺规作三角形,有三种基本类型:
(1)已知三角形的两边及其夹角,求作符合要求的三角形,其作图依据是“____”;
(2)已知三角形的两角及其夹边,求作符合要求的三角形,其作图依据是“____”;
(3)已知三角形的三边,求作符合要求的三角形,其作图依据是“____”.
SAS ASA SSS
【解析】根据SAS—两边及其夹角分别相等的两个三角形全等；ASA—两角及其夹边分别相等的两个三角形全等；SSS—三边分别相等的两个三角形全等.
故答案：(1)SAS、 (2)ASA 、(3)SSS. 已知tanβ=22.3，则β=_________（精确到1″）
87°25′56″
【解析】试题分析：利用计算器首先按2ndF，再按tan，再输入22.3，再按DMS即可得出答案．
∵tanβ=22.3，∴β=87°25′56″．
故答案为：87°25′56″