题目内容
一堆有红、白两种颜色的球若干个，已知白球的个数比红球少，但白球的2倍比红球多．若把每一个白球都记作“2”，每一个红球都记作“3”，则总数为“60”，那么这两种球各有多少个？
白球有9个，红球有14个．
【解析】【试题分析】设白球有x个，红球有y个，根据“白球的个数比红球少，但白球的2倍比红球多”，得 ，解得7.5＜x＜12，则x可以取8,9,10,11.
由于2x=60－3y=3（20－y） 得2x应是3的倍数，则x只能取9，y = = 14
即白球有9个，红球有14个．
【试题解析】
设白球有x个，红球有y个，由题意，得
由第一个...
练习册系列答案
相关题目
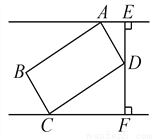
如图，矩形ABCD是供一机动车停放的车位示意图，已知BC＝2m，CD＝5.4m，∠DCF＝30°.请你计算车位所占的宽度EF约为多少米？(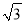
≈1.73，结果保留一位小数)
4.4米
【解析】试题分析：分别在Rt△BCF和Rt△AEF中求得DF和DE的长后，相加即可得到EF的长．
试题解析：
在Rt△DCF中，
∵CD=5.4m，∠DCF=30°，
∴sin∠DCF=，
∴DF=2.7m，
∵∠CDF+∠DCF=90°∠ADE+∠CDF=90°，
∴∠ADE=∠DCF=30°，
∵AD=BC=2，
∴cos∠... 某口袋中有20个球,每个球除颜色外都相同,其中白球x个,绿球2x个,其余为黑球,甲从袋中任意摸出一个球,若为绿球则获胜,甲摸出的球放回袋中,乙从袋中摸出一个球,若为黑球则获胜.若对甲、乙双方公平,则x等于( )
A. 3 B. 4 C. 5 D. 6
B
【解析】【解析】
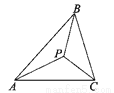
根据题意得： ，即2x=20-x-2x，解得：x=4．故选B． 如图，在△ABC中，点P是△ABC三条角平分线的交点，则∠PBC＋∠PCA＋∠PAB=___度．
90
【解析】试题分析：由在△ABC中，点P是△ABC的内心，根据三角形的内心是三角形三条角平分线的交点，即可得∠PBC=∠ABC，∠PCA=∠ACB，∠PAB=∠BAC，又由三角形内角和定理，即可求得∠PBC+∠PCA+∠PAB的度数．
试题解析：∵在△ABC中，点P是△ABC的内心，
∴∠PBC=∠ABC，∠PCA=∠ACB，∠PAB=∠BAC，
∵∠ABC+∠BCA+... 如图，已知△ABC的六个元素，则下列甲、乙、丙三个三角形中和△ABC全等的图形是( )
A. 甲、乙 B. 甲、丙
C. 乙、丙 D. 甲、乙、丙
C
【解析】试题解析：由图形可知，甲有一边一角，不能判断两三角形全等，
乙有两边及其夹角，能判断两三角形全等，
丙得出两角及其一角对边，能判断两三角形全等，
根据全等三角形的判定得，乙丙正确.
故选C. 求不等式1＋x＞x－1成立的x取值范围.
x可取一切实数
【解析】
试题分析：根据不等式的基本性质求出不等式1＋x＞x－1的解集即可判断.
不等式1＋x＞x－1两边同时减去x得1＞－1，恒成立
则不等式1＋x＞x－1成立的x取值范围是x可取一切实数. 不等式－2x＜8的负整数解的和是______．
－6
【解析】解不等式－2x＜8 得： ，则它的负整数解为x=-1,-2,-3,故原不等式的负整数解的和为 .故答案为-6. 如图是数轴的一部分,其单位长度为a,已知在△ABC中,AB=3a,BC=4a,AC=5a.用直尺和圆规作出△ABC(要求:使点A,C在数轴上,保留作图痕迹,不必写出作法).
见解析
【解析】【试题分析】利用“SSS”作出三角形，作图方法见解析.
【试题解析】
如图.
作法如下:
(1)在数轴上截取AC=5a.
(2)分别以A,C为圆心,以3a,4a为半径画弧,两弧相交于点B.
(3)连接AB,BC,则△ABC即为所求作的三角形. 在图示的四个汽车标志图案中，能用平移变换来分析其形成过程的图案是( )
A. 
B. 
C. 
D. 
D
【解析】试题分析：根据平移的概念，即平移前后图形的大小，形状都不变，只是位置改变.
故选D.