题目内容
11.甲、乙两人参加理化实验操作测试,学校进行了6次模拟测试,成绩如表所示.| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 平均分 | 众数 | |
| 甲 | 7 | 9 | 9 | 9 | 10 | 10 | 9 | 9 |
| 乙 | 7 | 8 | 9 | 10 | 10 | 10 | 9 | 10 |
(2)已知甲成绩的方差等于1,请计算乙成绩的方差;
(3)从平均数和方差相结合看,分析谁的成绩好些?
分析 (1)根据平均数的计算公式和众数的定义进行解答即可;
(2)根据方差公式列出算式,再进行计算即可;
(3)根据方差的意义方差越大,波动性越大,反之也成立,解答即可.
解答 解:(1)乙的平均数是:(7+8+9+10+10+10)÷6=9;
∵10出现了3次,出现的次数最多,
∴乙的众数是10;
故答案为:9,10;
(2)乙的方差是:$\frac{1}{6}$[(7-9)2+(8-9)2+(9-9)2+3(10-9)2]=$\frac{4}{3}$;
(3)甲的成绩好鞋些,因为两个人的平均成绩都是9分,但甲的方差小,成绩更稳定.
点评 本题考查方差、平均数和众数:一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立;众数的一组数据中出现次数最多的数.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
2. 如图,已知四边形ABCD是平行四边形,要使它成为菱形,那么需要添加的条件可以是( )
如图,已知四边形ABCD是平行四边形,要使它成为菱形,那么需要添加的条件可以是( )
 如图,已知四边形ABCD是平行四边形,要使它成为菱形,那么需要添加的条件可以是( )
如图,已知四边形ABCD是平行四边形,要使它成为菱形,那么需要添加的条件可以是( )| A. | AC⊥BD | B. | AB=AC | C. | ∠ABC=90° | D. | AC=BD |
19.下列运算正确的是( )
| A. | a+2a=2a2 | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | (x-3)2=x2-9 | D. | -2-2=-$\frac{1}{4}$ |
 如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,若把Rt△ABC绕AC边所在直线旋转一周,则所得圆锥的体积是12π.
如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,若把Rt△ABC绕AC边所在直线旋转一周,则所得圆锥的体积是12π. 已知:如图,在△AOB中,OB=OA,∠AOB=90°.在△ACQ中,AC=CQ,∠ACQ=90°,点P为BQ的中点
已知:如图,在△AOB中,OB=OA,∠AOB=90°.在△ACQ中,AC=CQ,∠ACQ=90°,点P为BQ的中点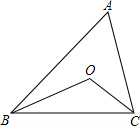 如图,∠ABC=40°,∠ACB=60°,BO、CO平分∠ABC和∠ACB,则∠BOC=130°.
如图,∠ABC=40°,∠ACB=60°,BO、CO平分∠ABC和∠ACB,则∠BOC=130°.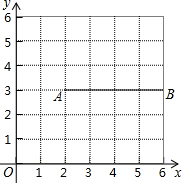 如图所示,在平面直角坐标系中,已知点A(2,3)、B(6,3),连接AB.如果点P在直线y=x-1上,且点P到直线AB的距离小于1,那么称点P是线段AB的“邻近点”.若点P(m,n)是线段AB的“邻近点”,则m的取值范围是3<m<5.
如图所示,在平面直角坐标系中,已知点A(2,3)、B(6,3),连接AB.如果点P在直线y=x-1上,且点P到直线AB的距离小于1,那么称点P是线段AB的“邻近点”.若点P(m,n)是线段AB的“邻近点”,则m的取值范围是3<m<5.