题目内容
4. 已知:如图,在△AOB中,OB=OA,∠AOB=90°.在△ACQ中,AC=CQ,∠ACQ=90°,点P为BQ的中点
已知:如图,在△AOB中,OB=OA,∠AOB=90°.在△ACQ中,AC=CQ,∠ACQ=90°,点P为BQ的中点(1)延长OP至点M,使PM=OP,连接CM,求证:CM=OC;
(2)判断△OMC的形状,写出并说明理由;
(3)判断QM与OA的位置关系,写出并说明理由.
分析 (1)欲证明CM=OC,只要证明△AOC≌△QMC即可.
(2)结论:△OCM是等腰直角三角形,只要证明∠OCM=∠ACQ即可.
(3)结论:QM⊥OA,利用“8字型”进行证明.
解答 (1)证明:在△BOP和△QMP中,
$\left\{\begin{array}{l}{OP=PM}\\{∠OPB=∠MPQ}\\{BP=PQ}\end{array}\right.$,
∴△BOP≌△QMP,
∴QM=OB=AO,∠MQP=∠OBP=45°+∠ABQ,
∵∠OAC=∠OAB+∠BAQ+∠QAC=90°+∠BAQ,
∠MQC=360°-∠AQC-∠AQB=∠BQM=360°-45°-(180°-∠QAB-∠ABQ)-(45°+∠ABQ)=90°+∠QAB.
∴∠MQC=∠OAC,
在△AOC和△QMC中,
$\left\{\begin{array}{l}{AO=QM}\\{∠OAC=∠MQC}\\{AC=CQ}\end{array}\right.$,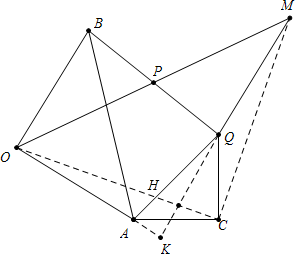
∴△AOC≌△QMC,
∴CM=CO,
(2)结论:△OCM是等腰直角三角形,理由:
证明:∵△AOC≌△QMC,
∴∠ACO=∠QCM,
∴∠OCM=∠ACQ=90°,
∵OC=CM,
∴△OCM是等腰直角三角形.
(3)结论:QM⊥OA,理由:
证明:延长MQ、OA交于点K,OC与KM交于点H,
∵△AOC≌△QMC,
∴∠CMQ=∠COK,
∵∠CMO+∠CHM=90°,∠CHM=∠OHK,
∴∠OHK+∠AOC=90°,
∴∠OKH=90°,
∴QM⊥OA.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质,正确寻找全等三角形是解决问题的关键,学会利用“8字型”证明直角,属于中考常考题型.

练习册系列答案
相关题目
6.计算(-12)÷4的结果是( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
4.已知m=8-$\sqrt{20}$,估算m的值所在的范围是( )
| A. | 1<m<2 | B. | 2<m<3 | C. | 3<m<4 | D. | 4<m<5 |
11.甲、乙两人参加理化实验操作测试,学校进行了6次模拟测试,成绩如表所示.
(1)根据图表信息,补全表格;
(2)已知甲成绩的方差等于1,请计算乙成绩的方差;
(3)从平均数和方差相结合看,分析谁的成绩好些?
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 平均分 | 众数 | |
| 甲 | 7 | 9 | 9 | 9 | 10 | 10 | 9 | 9 |
| 乙 | 7 | 8 | 9 | 10 | 10 | 10 | 9 | 10 |
(2)已知甲成绩的方差等于1,请计算乙成绩的方差;
(3)从平均数和方差相结合看,分析谁的成绩好些?
13.下列因式分解正确的是( )
| A. | x3-x=x(x2-1) | B. | a2-8a+16=(a-4)2 | C. | 5x2+5y2=5(x+y)2 | D. | m2+m-6=(m-3)(m+2) |
14.下列二次根式中,是最简二次根式的是( )
| A. | $\sqrt{0.2b}$ | B. | $\sqrt{12a-12b}$ | C. | $\sqrt{x2-y2}$ | D. | $\sqrt{5ab2}$ |