题目内容
11．
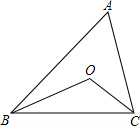如图，∠ABC=40°，∠ACB=60°，BO、CO平分∠ABC和∠ACB，则∠BOC=130°．
分析 根据角平分线的定义可求出∠OBC和∠OCB，然后利用三角形内角和定理就可求出∠BOC．
解答 解∵BO、CO平分∠ABC和∠ACB，
∴∠OBC=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×40°=20°，∠OCB=$\frac{1}{2}$∠ACB=$\frac{1}{2}$×60°=30°，
∴∠BOC=180°-∠OBC-∠OCB=180°-20°-30°=130°．
故答案为130°．
点评 本题主要考查了角平分线的定义、三角形内角和定理等知识，在三角形中求角度，通常需利用三角形内角和定理和外角的性质．
练习册系列答案
阅读快车系列答案
相关题目
14．
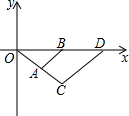如图，△OAB与△OCD是以点O为位似中心的位似图形，相似比为1：2，∠OCD=90°，CO=CD，若B（1，0），则点C的坐标为（ ）
如图，△OAB与△OCD是以点O为位似中心的位似图形，相似比为1：2，∠OCD=90°，CO=CD，若B（1，0），则点C的坐标为（ ）| A． | （1，-2） | B． | （-2，1） | C． | （$\sqrt{2}，-\sqrt{2}$） | D． | （1，-1） |
11．甲、乙两人参加理化实验操作测试，学校进行了6次模拟测试，成绩如表所示．
（1）根据图表信息，补全表格；
（2）已知甲成绩的方差等于1，请计算乙成绩的方差；
（3）从平均数和方差相结合看，分析谁的成绩好些？
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 平均分 | 众数 | |
| 甲 | 7 | 9 | 9 | 9 | 10 | 10 | 9 | 9 |
| 乙 | 7 | 8 | 9 | 10 | 10 | 10 | 9 | 10 |
（2）已知甲成绩的方差等于1，请计算乙成绩的方差；
（3）从平均数和方差相结合看，分析谁的成绩好些？
6．下列计算正确的是（ ）
| A． | 2a-a=2 | B． | m6÷m2=m3 | ||
| C． | x2010+x2010=2x2010 | D． | t2-t3=t6 |