题目内容
10.解方程组:$\left\{\begin{array}{l}x+3y=6\\{x^2}-4xy+4{y^2}=1.\end{array}\right.$.分析 由方程②可得(x-2y)2=1即x-2y=1或x-2y=-1,将原方程组分为$\left\{\begin{array}{l}x+3y=6\\ x-2y=1\end{array}\right.$或$\left\{\begin{array}{l}x+3y=6\\ x-2y=-1\end{array}\right.$,分别解每个方程组可得.
解答 解:在方程组$\left\{\begin{array}{l}{x+3y=6}&{①}\\{{x}^{2}-4xy+4{y}^{2}=1}&{②}\end{array}\right.$中,
由②得:(x-2y)2=1,
∴x-2y=1或x-2y=-1,
所以原方程组变为:$\left\{\begin{array}{l}x+3y=6\\ x-2y=1\end{array}\right.$或$\left\{\begin{array}{l}x+3y=6\\ x-2y=-1\end{array}\right.$,
解这两个方程组得:$\left\{\begin{array}{l}x=3\\ y=1\end{array}\right.$,$\left\{\begin{array}{l}x=\frac{9}{5}\\ y=\frac{7}{5}\end{array}\right.$
所以原方程组的解为$\left\{\begin{array}{l}{x_1}=3\\{y_2}=1\end{array}\right.$,$\left\{\begin{array}{l}{x_2}=\frac{9}{5}\\{y_2}=\frac{7}{5}\end{array}\right.$.
点评 本题主要考查解高次方程组的能力,体现了化归思想在解高次方程或多元方程中的应用,解高次方程需降幂,多元方程需消元.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案| A. | $\sqrt{3}$,2,$\sqrt{5}$ | B. | 0.7,2.4,2.5 | C. | 6,8,10 | D. | 9,12,15 |
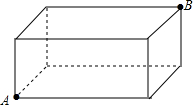 已知长方体的长、宽、高分别为30cm、20cm、10cm,一只蚂蚁从A处出发到B处觅食,求它所走的最短路径.(结果保留根号)
已知长方体的长、宽、高分别为30cm、20cm、10cm,一只蚂蚁从A处出发到B处觅食,求它所走的最短路径.(结果保留根号)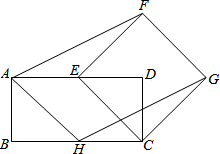 如图,矩形ABCD和正方形ECGF.其中E、H分别为AD、BC中点.连结AF、HG、AH.
如图,矩形ABCD和正方形ECGF.其中E、H分别为AD、BC中点.连结AF、HG、AH.