题目内容

20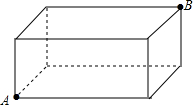．已知长方体的长、宽、高分别为30cm、20cm、10cm，一只蚂蚁从A处出发到B处觅食，求它所走的最短路径．（结果保留根号）

分析 因为平面展开图不唯一，故分情况分别计算，进行大、小比较，再从各个路线中确定最短的路线．

解答 解：长方体的展开图如图：

（1）展开前面右面由勾股定理得AB2=（30+20）2+102=2600；
（2）展开前面上面由勾股定理得AB2=（10+20）2+302=1800；
（3）展开左面上面由勾股定理得AB2=（10+30）2+202=2000．
∵30$\sqrt{2}$＜20$\sqrt{5}$＜10$\sqrt{26}$，
∴最短路程长为30$\sqrt{2}$cm．

点评 本题考查的是平面展开-最短路径问题，根据题意画出长方体的侧面展开图，利用勾股定理求解是解答此题的关键．

练习册系列答案
相关题目
10．我们知道平方运算和开方运算是互逆运算，如：a2±2ab+b2=（a±b）2，那么$\sqrt{{a}^{2}±2ab+{b}^{2}}$=|a±b|，那么如何将双重二次根式$\sqrt{a±2\sqrt{b}}$（a＞0，b＞0，a±2$\sqrt{b}$＞0）化简呢？如能找到两个数m，n（m＞0，n＞0），使得（$\sqrt{m}$）2+（$\sqrt{n}$）2=a即m+n=a，且使$\sqrt{m}$$•\sqrt{n}$=$\sqrt{b}$即m•n=b，那么a±2$\sqrt{b}$=（$\sqrt{m}$）2+（$\sqrt{n}$）2±2$\sqrt{m}$•$\sqrt{n}$=（$\sqrt{m}$±$\sqrt{n}$）2∴$\sqrt{a±2\sqrt{b}}$=|$\sqrt{m}$±$\sqrt{n}$，双重二次根式得以化简；
例如化简：$\sqrt{3+2\sqrt{2}}$；∵3=1+2 且2=1×2，∴3+2$\sqrt{2}$=（$\sqrt{1}$）2+（$\sqrt{2}$）2+2$\sqrt{1}$×$\sqrt{2}$∴$\sqrt{3+2\sqrt{2}}$=1+$\sqrt{2}$
由此对于任意一个二次根式只要可以将其化成$\sqrt{a±2\sqrt{b}}$的形式，且能找到m，n（m＞0，n＞0）使得m+n=a，且m•n=b，那么这个双重二次根式一定可以化简为一个二次根式．请同学们通过阅读上述材料，完成下列问题：
（1）填空：$\sqrt{5-2\sqrt{6}}$=$\sqrt{3}$-$\sqrt{2}$；$\sqrt{12+2\sqrt{35}}$=$\sqrt{5}$+$\sqrt{7}$；
（2）化简：①$\sqrt{9+6\sqrt{2}}$   ②$\sqrt{16-4\sqrt{15}}$
（3）计算：$\sqrt{3-\sqrt{5}}$+$\sqrt{2+\sqrt{3}}$．
11．方程-2x+3=0的解是（　　）
A．$\frac{2}{3}$B．-$\frac{2}{3}$C．$\frac{3}{2}$D．-$\frac{3}{2}$
8．解方程：
（1）3（2x-1）-2（1-x）=-1
（2）$\frac{y-1}{2}$=2-$\frac{y+2}{5}$．
15．下列能构成直角三角形的一组数是（　　）
A．2、3、4B．6、8、9C．5、12、13D．1、1、2
5．下列四组线段中，可以构成直角三角形的是（　　）
A．6，7，8B．1，$\sqrt{2}$，5C．6，8，10D．$\sqrt{5}$，2$\sqrt{3}$，$\sqrt{15}$
12．下列语句是真命题的是（　　）
A．同位角相等B．如果a⊥b，b⊥c，则a⊥c
C．相等的角是对顶角D．如果a∥b，b∥c，则a∥c
9．计算：
（1）3$\sqrt{2}$-|$\sqrt{3}$-$\sqrt{2}$|
（2）$3\sqrt{3}$+$2\sqrt{3}$．
10．解方程组：$\left\{\begin{array}{l}x+3y=6\\{x^2}-4xy+4{y^2}=1.\end{array}\right.$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网