题目内容
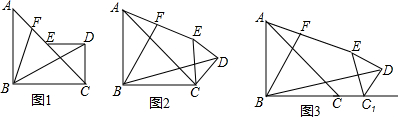
20.如图1,在等腰直角△ABC和等腰直角△CDE中,∠ABC,∠CDE是直角,连接BD,点F在AE上且∠FBD=45°,AB=2,CD=1.(1)求证:AF=FE;
(2)若将等腰直角CDE绕点C旋转一个a(0°<a≤90°)角,其它条件不变,如图2,求$\frac{AF}{FE}$的值;
(3)在(2)的条件下,再将等腰直角△CDE沿直线BC右移k个单位,其它条件不变,如图3,试求$\frac{AF}{FE}$的值(用含k的代数式表示)
分析 (1)由辅助线得到BD=GD,再判断出△ABF≌△EGF,△ABF≌△EGF即可;
(2)由辅助线得到BD=GD,再判断出△ABF≌△EGF,△ABF≌△EGF即可;
(3)由辅助线得到BD=GD,再判断出△BC1D≌△GED,从而得出△ABF∽△EGF即可.
解答 解:(1)证明:过D作DG垂直于BD交BF的延长线于G,连结EG
∵∠FBD=45°,
∴△BDG为等腰直角三角形,
∴BD=GD,
∵∠BDC=90°-∠BDE=∠GDE,CD=ED,
∴△BCD≌△GED,
∴BC=GE,∠DBC=∠DGE,
∴AB=BC=EG,∠ABF=45°-∠DBC=45°-∠DGE=∠EGF,
∴△ABF≌△EGF,
∴AF=EF,
即AF=FE.
(2)$\frac{AF}{EF}$=1.
如图2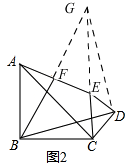
过D作DG垂直于BD交BF的延长线于G,连结EG,
∵∠FBD=45°,
∴△BDG为等腰直角三角形,
∴BD=GD,
又∵∠BDC=90°-∠BDE=∠GDE,CD=ED,
∴△BCD≌△GED,
∴BC=GE,∠DBC=∠DGE,
∴AB=BC=EG,∠ABF=45°-∠DBC=45°-∠DGE=∠EGF,
∴△ABF≌△EGF,
∴AF=EF,
即AF=FE.
∴$\frac{AF}{EF}$=1.
(3)$\frac{AF}{EF}=\frac{2}{k+2}$.
如图3,
过D作DG垂直于BD交BF的延长线于G,连结EG
∵∠FBD=45°,
∴△BDG为等腰直角三角形,
∴BD=GD,
∵∠BDC=90°-∠BDE=∠GDE,C1D=ED,
∴△BC1D≌△GED,
∵BC1=GE,∠ABF=45°-∠DBC=45°-∠DGE=∠EGF,
∴△ABF∽△EGF,
∴$\frac{AF}{EF}=\frac{AB}{EG}$,
∵AB=2,BC1=k+2,
$\frac{AF}{EF}=\frac{AB}{EG}$=$\frac{2}{k+2}$.
点评 此题是几何变换综合题,主要考查了等腰直角三角形的性质,三角形的全等的判定和性质,相似三角形的性质和判定,作出辅助线,判断出三角形相似是解本题的关键.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案| A. | 1-x-3=3x | B. | 6-2x-6=3x | C. | 6-x+3=3x | D. | 1-x+3=3x |
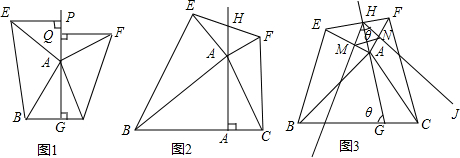
 如图,在梯形ABCD中,∠ABC=∠BAD=90°,在AD上取一点E,将△ABE沿直线BE折叠,使点A落在BD上的G处,EG的延长线交直线BC于点F.
如图,在梯形ABCD中,∠ABC=∠BAD=90°,在AD上取一点E,将△ABE沿直线BE折叠,使点A落在BD上的G处,EG的延长线交直线BC于点F. 已知直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=DC=5,点P在BC上移动,则当PA+PD取最小值时,BP长为( )
已知直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=DC=5,点P在BC上移动,则当PA+PD取最小值时,BP长为( )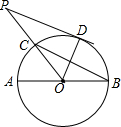 如图,AB是⊙O的直径,BC是弦,∠ABC=30°,连结OC并延长至点P,使CP=OC,过点P作⊙O的切线,D是切点.
如图,AB是⊙O的直径,BC是弦,∠ABC=30°,连结OC并延长至点P,使CP=OC,过点P作⊙O的切线,D是切点. 如图,在平行四边形ABCD中,AB⊥AC,点E是AC上一点,且AE=AB,连接BE交BC边上的高AF于点H,延长对角线CA至点G.使AG=CE,连接GH.求证:∠CAD=∠G.
如图,在平行四边形ABCD中,AB⊥AC,点E是AC上一点,且AE=AB,连接BE交BC边上的高AF于点H,延长对角线CA至点G.使AG=CE,连接GH.求证:∠CAD=∠G.