题目内容
5.已知反比例函数y=$\frac{k}{x}$的图象经过(-1,-2)(1)求这个函数的解析式;
(2)若点(2,n)在这个函数图象上,求n的值.
分析 (1)直接把点(-1,-2)代入反比例函数y=$\frac{k}{x}$即可得出结论.
(2)把(2,n)代入强大的解析式即可求得.
解答 解:(1)∵反比例函数y=$\frac{k}{x}$的图象经过(-1,-2),
∴-2=$\frac{k}{-1}$,解得k=2.
∴这个函数的解析式为y=$\frac{2}{x}$.
(2)把(2,n)代入y=$\frac{2}{x}$得n=$\frac{2}{2}$=1.
点评 本题考查的是待定系数法求反比例函数的解析式以及反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.下列能构成直角三角形的一组数是( )
| A. | 2、3、4 | B. | 6、8、9 | C. | 5、12、13 | D. | 1、1、2 |
16.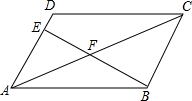 如图,在平行四边形ABCD中,AE:AD=2:3,连接BE交AC于点F,若△ABF和四边形CDEF的面积分别记为S1,S2,则S1:S2为( )
如图,在平行四边形ABCD中,AE:AD=2:3,连接BE交AC于点F,若△ABF和四边形CDEF的面积分别记为S1,S2,则S1:S2为( )
 如图,在平行四边形ABCD中,AE:AD=2:3,连接BE交AC于点F,若△ABF和四边形CDEF的面积分别记为S1,S2,则S1:S2为( )
如图,在平行四边形ABCD中,AE:AD=2:3,连接BE交AC于点F,若△ABF和四边形CDEF的面积分别记为S1,S2,则S1:S2为( )| A. | 2:3 | B. | 4:9 | C. | 6:11 | D. | 6:13 |
13. 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交FG于点P,则DP等于( )
如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交FG于点P,则DP等于( )
 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交FG于点P,则DP等于( )
如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交FG于点P,则DP等于( )| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 2 | D. | 1 |
17.已知矩形的一组邻边为3和4,那么这个矩形的对角线长是( )
| A. | 7 | B. | 12 | C. | 5 | D. | 3.5 |
15.解方程$1-\frac{x+3}{3}=\frac{x}{2}$时,去分母后可以得到( )
| A. | 1-x-3=3x | B. | 6-2x-6=3x | C. | 6-x+3=3x | D. | 1-x+3=3x |