题目内容
15.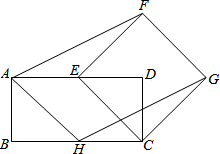 如图,矩形ABCD和正方形ECGF.其中E、H分别为AD、BC中点.连结AF、HG、AH.
如图,矩形ABCD和正方形ECGF.其中E、H分别为AD、BC中点.连结AF、HG、AH.(1)求证:AF=HG;
(2)求证:∠FAD=∠GHC;
(3)试探究∠FAH与∠AFE的关系.
分析 (1)根据矩形的性质和已知得出AE=HC,AE∥HC,求出四边形AHCE为平行四边形,根据平行四边形的性质得出AH=EC,AH∥EC,求出四边形AHGF是平行四边形,即可得出答案;
(2)根据平行线得出∠FAH+∠AHG=180°,求出∠DAH=∠AHB,根据∠AHB+∠AHG+∠GHC=180°即可得出答案;
(3)过A点作AM∥EF,根据平行线的性质得出∠MAF=∠AFE,求出MA⊥AH,根据垂直得出∠MAF+∠FAH=90°,即可得出答案.
解答 (1)证明:∵四边形ABCD是矩形,且E、H分别为AD、BC的中点,
∴AE=HC,AE∥HC,
∴四边形AHCE为平行四边形,
∴AH=EC,AH∥EC,
又∵四边形ECGF为正方形,
∴EC=FG,EC∥FG,
∴AH=FG,AH∥FG,
∴四边形AHGF是平行四边形,
∴AH=FG;
(2)证明:∵四边形AHGF是平行四边形,
∴∠FAH+∠AHG=180°,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAH=∠AHB,
又∵∠AHB+∠AHG+∠GHC=180°,
∴∠FAD=∠GHC;
(3)∠FAH+∠AFE=90°,
证明:过A点作AM∥EF,
则∠MAF=∠AFE,
∵AM∥EF,AH∥EC,FE⊥EC,
∴MA⊥AH,
∴∠MAF+∠FAH=90°,
∴∠FAH+∠AFE=90°.
点评 本题考查了矩形的性质,平行四边形的性质和判定,正方形的性质的应用,能综合运用知识点进行推理是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.下列四组线段中,可以构成直角三角形的是( )
| A. | 6,7,8 | B. | 1,$\sqrt{2}$,5 | C. | 6,8,10 | D. | $\sqrt{5}$,2$\sqrt{3}$,$\sqrt{15}$ |
6.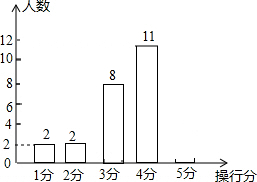 某班有50名同学,男、女生人数各占一半.在本周操行评定中,该班操行得分情况见如下统计表;其中男生操行得分情况见如下不完整的条形统计图:
某班有50名同学,男、女生人数各占一半.在本周操行评定中,该班操行得分情况见如下统计表;其中男生操行得分情况见如下不完整的条形统计图:
(1)补全条形统形图;
(2)若要在操行得分为5分的4名同学中选出两名同学作“本周操行明星”,用画树状图或列表的方法求出选为“本周操行明星”的正好是一名男同学和一名女同学的概率.
 某班有50名同学,男、女生人数各占一半.在本周操行评定中,该班操行得分情况见如下统计表;其中男生操行得分情况见如下不完整的条形统计图:
某班有50名同学,男、女生人数各占一半.在本周操行评定中,该班操行得分情况见如下统计表;其中男生操行得分情况见如下不完整的条形统计图:| 操行分得分 | 1分 | 2分 | 3分 | 4分 | 5分 |
| 人 数 | 2 | 4 | 10 | 30 | 4 |
(2)若要在操行得分为5分的4名同学中选出两名同学作“本周操行明星”,用画树状图或列表的方法求出选为“本周操行明星”的正好是一名男同学和一名女同学的概率.
4.下列事件中,不确定事件是( )
| A. | a是实数,且|a|≥0 | B. | $\frac{1}{2}$+$\frac{x-1}{5}$=0不是分式方程 | ||
| C. | 三角形内角和等于360° | D. | a是实数,a0=1 |
 如图,在梯形ABCD中,∠ABC=∠BAD=90°,在AD上取一点E,将△ABE沿直线BE折叠,使点A落在BD上的G处,EG的延长线交直线BC于点F.
如图,在梯形ABCD中,∠ABC=∠BAD=90°,在AD上取一点E,将△ABE沿直线BE折叠,使点A落在BD上的G处,EG的延长线交直线BC于点F.