题目内容

19．对于两个不相等的实数a、b，我们规定符号Max{a，b}表示a、b中的较大值，例如：Max{2，4}=4，按照这个规定，求方程Max{x，-x}=$\frac{2x+1}{x}$的解．

分析 根据题中的新定义，将所求方程化简，计算即可求出解．

解答 解：当x＞-x，即x＞0时，所求方程变形得：x=$\frac{2x+1}{x}$，即x2-2x-1=0，解得：x1=1+$\sqrt{2}$，x2=1-$\sqrt{2}$（舍去）；
当x＜-x，即x＜0时，所求方程变形得：-x=$\frac{2x+1}{x}$，即x2+2x+1=0，解得：x3=x4=-1，
经检验：x1=1+$\sqrt{2}$，x3=x4=-1都为分式方程的解．

点评 此题考查了分式方程的解，弄清题中的新定义是解本题的关键．

练习册系列答案
相关题目
9．计算：
（1）3$\sqrt{2}$-|$\sqrt{3}$-$\sqrt{2}$|
（2）$3\sqrt{3}$+$2\sqrt{3}$．
10．解方程组：$\left\{\begin{array}{l}x+3y=6\\{x^2}-4xy+4{y^2}=1.\end{array}\right.$．
7．如图1，抛物线y=-x2+$\frac{7}{2}x+2$与直线l1：y=-$\frac{1}{2}$x-3交于点A，点A的横坐标为-1，直线l1与x轴的交点为D，将直线l1向上平移后得到直线l2，直线l2刚好经过抛物线与x轴正半轴的交点B和与y轴的交点C．
（1）直接写出点A和点D的坐标，并求出点B的坐标；
（2）若点M是抛物线第一象限内的一个动点，连接DM，交直线l2于点N，连接AM和AN．设△AMN的面积为S，当S取得最大值时，求出此时点M的坐标及S的最大值；
（3）如图2，动点P以每秒1个单位长度的速度从点O出发，沿射线OB运动；同时，动点Q以每秒$\sqrt{5}$个单位长度的速度从点C出发，沿射线CB运动，设运动时间为t（t＞0）．过P点作PH⊥x轴，交抛物线于点H，当点P、Q、H所组成的三角形是直角三角形时，直接写出t的值．
14．计算：若ab＞0，求$\frac{a}{|a|}$+$\frac{b}{|b|}$+$\frac{|ab|}{ab}$的值．
4．下列事件中，不确定事件是（　　）
A．a是实数，且|a|≥0B．$\frac{1}{2}$+$\frac{x-1}{5}$=0不是分式方程
C．三角形内角和等于360°D．a是实数，a0=1
11．把下列方程整理成一元二次方程的一般形式，并写出常数项、一次项系数和二次项系数．
（1）-x2-4（2x-3）=9；
（2）3x（x-1）=5（x+2）
8．【特例发现】如图1，在△ABC中，AG⊥BC于点G，以A为直角顶点，分别以AB，AC为直角边，向△ABC外作等腰Rt△ABE和等腰Rt△ACF，过点E、F作射线GA的垂线，垂足分别为P、Q．求证：EP=FQ．
【延伸拓展】如图2，在△ABC中，AG⊥BC于点G，以A为直角顶点，分别以AB，AC为直角边，向△ABC外作Rt△ABE和Rt△ACF，射线GA交EF于点H．若AB=kAE，AC=kAF，请思考HE与HF之间的数量关系，并直接写出你的结论．
【深入探究】如图3，在△ABC中，G是BC边上任意一点，以A为顶点，向△ABC外作任意△ABE和△ACF，射线GA交EF于点H．若∠EAB=∠AGB，∠FAC=∠AGC，AB=kAE，AC=kAF，上一问的结论还成立吗？并证明你的结论．
【应用推广】在上一问的条件下，设大小恒定的角∠IHJ分别与△AEF的两边AE、AF分别交于点M、N，若△ABC为腰长等于4的等腰三角形，其中∠BAC=120°，且∠IHJ=∠AGB=θ=60°，k=2；
求证：当∠IHJ在旋转过程中，△EMH、△HMN和△FNH均相似，并直接写出线段MN的最小值（请在答题卡的备用图中补全作图）．
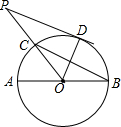9．如图，AB是⊙O的直径，BC是弦，∠ABC=30°，连结OC并延长至点P，使CP=OC，过点P作⊙O的切线，D是切点．
（Ⅰ）求证：PD∥BC；
（Ⅱ）当BC=3时，求PD的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网