题目内容
1.已知等式$\sqrt{x-2}+\root{3}{{{{(2-x)}^3}}}=0$在实数范围内成立,则x的值为2或3.分析 原式根据立方根性质可得$\sqrt{x-2}$=x-2,而算术平方根等于其本身的只有0和1,列出方程求解可得.
解答 解:由等式$\sqrt{x-2}+\root{3}{{{{(2-x)}^3}}}=0$可得,
$\sqrt{x-2}$+2-x=0,即:$\sqrt{x-2}$=x-2,
∴x-2=0或x-2=1,
解得:x=2或x=3,
故答案为:2或3.
点评 本题主要考查平方根、立方根,数量掌握平方根、立方根的性质是解题的根本和关键.

练习册系列答案
相关题目
11.方程-2x+3=0的解是( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
12.下列语句是真命题的是( )
| A. | 同位角相等 | B. | 如果a⊥b,b⊥c,则a⊥c | ||
| C. | 相等的角是对顶角 | D. | 如果a∥b,b∥c,则a∥c |
16.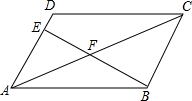 如图,在平行四边形ABCD中,AE:AD=2:3,连接BE交AC于点F,若△ABF和四边形CDEF的面积分别记为S1,S2,则S1:S2为( )
如图,在平行四边形ABCD中,AE:AD=2:3,连接BE交AC于点F,若△ABF和四边形CDEF的面积分别记为S1,S2,则S1:S2为( )
 如图,在平行四边形ABCD中,AE:AD=2:3,连接BE交AC于点F,若△ABF和四边形CDEF的面积分别记为S1,S2,则S1:S2为( )
如图,在平行四边形ABCD中,AE:AD=2:3,连接BE交AC于点F,若△ABF和四边形CDEF的面积分别记为S1,S2,则S1:S2为( )| A. | 2:3 | B. | 4:9 | C. | 6:11 | D. | 6:13 |
6.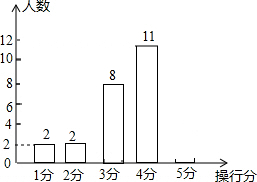 某班有50名同学,男、女生人数各占一半.在本周操行评定中,该班操行得分情况见如下统计表;其中男生操行得分情况见如下不完整的条形统计图:
某班有50名同学,男、女生人数各占一半.在本周操行评定中,该班操行得分情况见如下统计表;其中男生操行得分情况见如下不完整的条形统计图:
(1)补全条形统形图;
(2)若要在操行得分为5分的4名同学中选出两名同学作“本周操行明星”,用画树状图或列表的方法求出选为“本周操行明星”的正好是一名男同学和一名女同学的概率.
 某班有50名同学,男、女生人数各占一半.在本周操行评定中,该班操行得分情况见如下统计表;其中男生操行得分情况见如下不完整的条形统计图:
某班有50名同学,男、女生人数各占一半.在本周操行评定中,该班操行得分情况见如下统计表;其中男生操行得分情况见如下不完整的条形统计图:| 操行分得分 | 1分 | 2分 | 3分 | 4分 | 5分 |
| 人 数 | 2 | 4 | 10 | 30 | 4 |
(2)若要在操行得分为5分的4名同学中选出两名同学作“本周操行明星”,用画树状图或列表的方法求出选为“本周操行明星”的正好是一名男同学和一名女同学的概率.
13. 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交FG于点P,则DP等于( )
如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交FG于点P,则DP等于( )
 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交FG于点P,则DP等于( )
如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交FG于点P,则DP等于( )| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 2 | D. | 1 |