题目内容
16.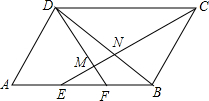 如图,?ABCD中,AE=EF=FB,CE交DF,DB于M,N,则EM:MN:NC=( )
如图,?ABCD中,AE=EF=FB,CE交DF,DB于M,N,则EM:MN:NC=( )| A. | 5:4:12 | B. | 5:3:12 | C. | 4:3:5 | D. | 2:1:4 |
分析 先根据平行四边形的性质得AB=CD,AB∥CD,则CD=3EF,EB:CD=2:3,再利用EF∥CD得到EM:MC=EF:CD=1:3,若设EM=t,则MC=3t,EC=4t,接着利用EB∥CD得到EN:NC=BE:CD=2:3,则可用t表示EN=$\frac{8}{5}$t,NC=$\frac{12}{5}$t,所以MN=EN-EM=$\frac{3}{5}$t,然后计算EM:MN:NC.
解答 解:∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
而AE=EF=FB,
∴CD=3EF,EB:CD=2:3,
∵EF∥CD,
∴EM:MC=EF:CD=1:3,
设EM=t,则MC=3t,EC=4t,
∵EB∥CD,
∴EN:NC=BE:CD=2:3,
∴EN=$\frac{2}{5}$CE=$\frac{8}{5}$t,NC=$\frac{3}{5}$EC=$\frac{12}{5}$t,
∴MN=EN-EM=$\frac{8}{5}$t-t=$\frac{3}{5}$t,
∴EM:MN:NC=t:$\frac{3}{5}$t:$\frac{12}{5}$t=5:3:12.
故选B.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;再运用相似三角形的性质时主要利用相似比计算线段的长.也考查了平行四边形的性质.

练习册系列答案
相关题目
4.整数m满足$\left\{\begin{array}{l}{2m-1>0}\\{4-2m>-1}\end{array}\right.$,则关于x的方程m2x2-4x-2=(m+2)x2+3x+4的解为( )
| A. | x1=-2,x2=-$\frac{3}{2}$ | B. | x1=2,x2=$\frac{3}{2}$ | ||
| C. | x1=-$\frac{6}{7}$ | D. | x1=-2,x2=-$\frac{3}{2}$,x3=-$\frac{6}{7}$ |
11.两个不等的实数a、b满足a2+a-1=0,b2+b-1=0,则ab的值为( )
| A. | 1 | B. | -1 | C. | $\frac{{-1±\sqrt{5}}}{2}$ | D. | $\sqrt{2}$ |
8.下列四组线段中,可以构成直角三角形的是( )
| A. | 4,5,6 | B. | 5,12,13 | C. | 2,3,4 | D. | 1,$\sqrt{2}$,3 |
5.一个几何体从三个方向看得到的图形如图所示,则这个几何体是( )


| A. | 圆柱 | B. | 圆锥 | C. | 长方体 | D. | 正方体 |
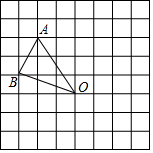 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABO的三个顶点都在格点上.
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABO的三个顶点都在格点上.