题目内容
11.两个不等的实数a、b满足a2+a-1=0,b2+b-1=0,则ab的值为( )| A. | 1 | B. | -1 | C. | $\frac{{-1±\sqrt{5}}}{2}$ | D. | $\sqrt{2}$ |
分析 由两个不等的实数a、b满足a2+a-1=0,b2+b-1=0知a、b可看做方程x2+x-1=0的两个不相等的实数根,由韦达定理可得答案.
解答 解:∵两个不等的实数a、b满足a2+a-1=0,b2+b-1=0,
∴a、b可看做方程x2+x-1=0的两个不相等的实数根,
∴ab=-1,
故选:B.
点评 本题主要考查根与系数的关系,根据题意得出a、b可看做方程x2+x-1=0的两个不相等的实数根是解题的关键.

练习册系列答案
相关题目
1.已知点A到直线BC的距离是4厘米,那么以点A为圆心4厘米为半径的圆与直线BC的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 无法确定 |
6.已知直线y=kx+3经过点A(-1,2)且与x轴交于点B,点B的坐标是( )
| A. | (-3,0) | B. | (0,3) | C. | (3,0) | D. | (0,-3) |
16.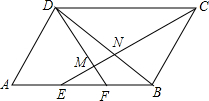 如图,?ABCD中,AE=EF=FB,CE交DF,DB于M,N,则EM:MN:NC=( )
如图,?ABCD中,AE=EF=FB,CE交DF,DB于M,N,则EM:MN:NC=( )
 如图,?ABCD中,AE=EF=FB,CE交DF,DB于M,N,则EM:MN:NC=( )
如图,?ABCD中,AE=EF=FB,CE交DF,DB于M,N,则EM:MN:NC=( )| A. | 5:4:12 | B. | 5:3:12 | C. | 4:3:5 | D. | 2:1:4 |
3.在平面直角坐标系中,A(1,$\sqrt{3}$),点O为坐标原点,则线段OA的长为( )
| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\sqrt{10}$ | D. | 4 |
1.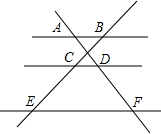 如图,已知AB∥CD∥EF,那么下列结论中正确的是( )
如图,已知AB∥CD∥EF,那么下列结论中正确的是( )
 如图,已知AB∥CD∥EF,那么下列结论中正确的是( )
如图,已知AB∥CD∥EF,那么下列结论中正确的是( )| A. | $\frac{CD}{EF}$=$\frac{AD}{AF}$ | B. | $\frac{AB}{CD}$=$\frac{BC}{EC}$ | C. | $\frac{AD}{BC}$=$\frac{AF}{BE}$ | D. | $\frac{CE}{BE}$=$\frac{AF}{AD}$ |