题目内容
15. 如图,一束光线从点O射出,照在经过A(1,0)、B(0,1)的镜面上的点D,经AB反射后,反射光线又照到竖立在y轴位置的镜面,经y轴再反射的光线恰好通过点A,则点D的坐标为($\frac{1}{3}$,$\frac{2}{3}$).
如图,一束光线从点O射出,照在经过A(1,0)、B(0,1)的镜面上的点D,经AB反射后,反射光线又照到竖立在y轴位置的镜面,经y轴再反射的光线恰好通过点A,则点D的坐标为($\frac{1}{3}$,$\frac{2}{3}$).
分析 应先作出点O及点A的像,过两个像的直线与直线AB的交点即为所求点.
解答 解:如图所示,
∵点O关于AB的对称点是O′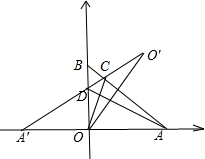 (1,1),
(1,1),
点A关于y轴的对称点是A′(-1,0)
设AB的解析式为y=kx+b,
∵(1,0),(0,1)在直线上,
∴$\left\{\begin{array}{l}{k+b=0}\\{b=1}\end{array}\right.$,解得k=-1,
∴AB的表达式是y=1-x,
同理可得O′A′的表达式是y=$\frac{x}{2}$+$\frac{1}{2}$,
两个表达式联立,解得x=$\frac{1}{3}$,y=$\frac{2}{3}$.
故答案为:($\frac{1}{3}$,$\frac{2}{3}$).
点评 本题考查了轴对称的知识;根据作相关点的像得到点D的位置是解决本题的关键.

练习册系列答案
相关题目
5.下列数据中最小的是( )
| A. | 11011001(二进制数) | B. | 75(十进制数) | ||
| C. | 72(八进制数) | D. | 57(十六制数) |
6.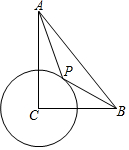 如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,则AP+$\frac{1}{2}$BP的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,则AP+$\frac{1}{2}$BP的最小值为( )
 如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,则AP+$\frac{1}{2}$BP的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,则AP+$\frac{1}{2}$BP的最小值为( )| A. | $\sqrt{37}$ | B. | 6 | C. | 2 $\sqrt{17}$ | D. | 4 |
20.估计$\sqrt{16}$+$\sqrt{20}$的运算结果应在( )
| A. | 6与7之间 | B. | 7与8之间 | C. | 8与9之间 | D. | 9与10之间 |
4. 如图,平行四边形ABCD中,对角线AC与BD相交于点O,且AB⊥AC,AB=3,OC=4,则BD的长为( )
如图,平行四边形ABCD中,对角线AC与BD相交于点O,且AB⊥AC,AB=3,OC=4,则BD的长为( )
 如图,平行四边形ABCD中,对角线AC与BD相交于点O,且AB⊥AC,AB=3,OC=4,则BD的长为( )
如图,平行四边形ABCD中,对角线AC与BD相交于点O,且AB⊥AC,AB=3,OC=4,则BD的长为( )| A. | 4 | B. | 5 | C. | 10 | D. | 12 |
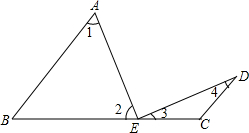 已知:如图,AB∥DC,点E是BC上一点,AB=BE,CD=CE.求证:AE⊥DE.
已知:如图,AB∥DC,点E是BC上一点,AB=BE,CD=CE.求证:AE⊥DE.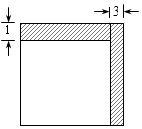 如图,悦悦将一张正方形纸片剪去一个宽为3cm的长方形纸条,再从剩下的长方形纸片上剪去一个宽为1cm的长条,如果第一次剪下的长方形纸条的周长恰好是第二次剪下的长方形纸条周长的2倍.
如图,悦悦将一张正方形纸片剪去一个宽为3cm的长方形纸条,再从剩下的长方形纸片上剪去一个宽为1cm的长条,如果第一次剪下的长方形纸条的周长恰好是第二次剪下的长方形纸条周长的2倍.