Question

6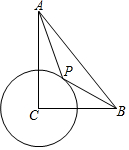．如图，在Rt△ABC中，∠ACB=90°，CB=4，CA=6，⊙C半径为2，P为圆上一动点，连结AP，BP，则AP+$\frac{1}{2}$BP的最小值为（　　）

• A． $\sqrt{37}$
• B． 6
• C． 2 $\sqrt{17}$
• D． 4

Answer 1

分析 连接CP，在CB上取点D，使CD=1，则有$\frac{CD}{CP}$=$\frac{CP}{CB}$=$\frac{1}{2}$，因为∠PCD=∠BCP，所以△PCD∽△BCP，所以$\frac{PD}{BP}$=$\frac{1}{2}$，推出PD=$\frac{1}{2}$BP，所以AP+$\frac{1}{2}$BP=AP+PD，要使AP+$\frac{1}{2}$BP最小，只要AP+AD最小，当点A，P，D在同一条直线时，AP+AD最小，即：AP+$\frac{1}{2}$BP最小值为AD，求出AD即可

解答 解：如图1，连接CP，在CB上取点D，使CD=1，则有$\frac{CD}{CP}$=$\frac{CP}{CB}$=$\frac{1}{2}$，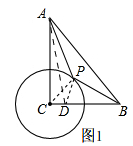

又∵∠PCD=∠BCP，
∴△PCD∽△BCP，
∴$\frac{PD}{BP}$=$\frac{1}{2}$，
∴PD=$\frac{1}{2}$BP，
∴AP+$\frac{1}{2}$BP=AP+PD．
要使AP+$\frac{1}{2}$BP最小，只要AP+AD最小，当点A，P，D在同一条直线时，AP+AD最小，
即：AP+$\frac{1}{2}$BP最小值为AD，
在Rt△ACD中，CD=1，AC=6，
∴AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{37}$，
AP+$\frac{1}{2}$BP的最小值为$\sqrt{37}$，
故选A．

点评 此题主要考查轴对称-最短问题、勾股定理，相似三角形的判定和性质、两点之间线段最短等知识，解题的关键是学会添加辅助线，构造相似三角形解决问题，属于中考常考题型．