题目内容
4. 如图,平行四边形ABCD中,对角线AC与BD相交于点O,且AB⊥AC,AB=3,OC=4,则BD的长为( )
如图,平行四边形ABCD中,对角线AC与BD相交于点O,且AB⊥AC,AB=3,OC=4,则BD的长为( )| A. | 4 | B. | 5 | C. | 10 | D. | 12 |
分析 利用平行四边形的性质和勾股定理易求BO的长,进而可求出BD的长.
解答 解:∵?ABCD的对角线AC与BD相交于点O,
∴BO=DO,AO=OC=4,
∵AB⊥AC,AB=3,
∴∠BAO=90°,
在Rt△ABO中,由勾股定理得:BO=$\sqrt{A{B}^{2}+O{A}^{2}}$=5,
∴BD=2BO=10,
故选:C.
点评 本题考查了平行四边形的性质以及勾股定理的运用,熟练掌握平行四边形的性质是解决问题的关键.

练习册系列答案
相关题目
12.一元二次方程x(x-2)=0的解是( )
| A. | x=2 | B. | x=0 | C. | x=0或x=2 | D. | x=0或x=-2 |
16.在以下四个标志中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.下列计算正确的是( )
| A. | a2+a2=a4 | B. | a8÷a2=a4 | C. | (-a)2-a2=0 | D. | a2•a3=a6 |
 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置. 如图,一束光线从点O射出,照在经过A(1,0)、B(0,1)的镜面上的点D,经AB反射后,反射光线又照到竖立在y轴位置的镜面,经y轴再反射的光线恰好通过点A,则点D的坐标为($\frac{1}{3}$,$\frac{2}{3}$).
如图,一束光线从点O射出,照在经过A(1,0)、B(0,1)的镜面上的点D,经AB反射后,反射光线又照到竖立在y轴位置的镜面,经y轴再反射的光线恰好通过点A,则点D的坐标为($\frac{1}{3}$,$\frac{2}{3}$). 如图,正方形ABCD的边长为2,点A与O重合,点C在y轴上,求正方形ABCD各顶点的坐标.
如图,正方形ABCD的边长为2,点A与O重合,点C在y轴上,求正方形ABCD各顶点的坐标.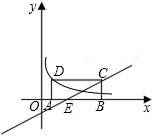 如图,矩形ABCD整体位于在第一象限,且点A、B在x轴正半轴上,AB=3,BC=1,直线y=$\frac{1}{2}$x-1经过点C交x轴于点E,双曲线经过点D,求此双曲线的表达式.
如图,矩形ABCD整体位于在第一象限,且点A、B在x轴正半轴上,AB=3,BC=1,直线y=$\frac{1}{2}$x-1经过点C交x轴于点E,双曲线经过点D,求此双曲线的表达式. 如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PC=6,则PD=3.
如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PC=6,则PD=3.