题目内容
7.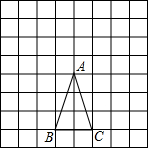 如图,在由完全相同的小正方形组成的网格中,△ABC的三个顶点都在格点上.
如图,在由完全相同的小正方形组成的网格中,△ABC的三个顶点都在格点上.(1)请在网格中找一个格点P,连接PB、PC,使∠BPC=$\frac{1}{2}$∠BAC,并简要说明理由;
(2)直接写出此时tan∠BPC的值.
分析 (1)图中点P即为所求.由AP=AB=AC,推出P、B、C在以P为圆心AP为半径的圆上,推出∠BPC=$\frac{1}{2}$∠BAC;
(2)作AK⊥BC于K,由AB=AC,推出∠BAK=$\frac{1}{2}$∠BAC=∠BPC,推出tan∠BPC=tan∠BAK=$\frac{BK}{AK}$=$\frac{1}{3}$即可;
解答 解:(1)图中点P即为所求.
理由:∵AP=AB=AC,
∴P、B、C在以P为圆心AP为半径的圆上,
∴∠BPC=$\frac{1}{2}$∠BAC.
(2)作AK⊥BC于K,
∵AB=AC,
∴∠BAK=$\frac{1}{2}$∠BAC=∠BPC,
∴tan∠BPC=tan∠BAK=$\frac{BK}{AK}$=$\frac{1}{3}$.
点评 本题考查作图-应用与设计,圆周角定理、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
2.下列各式中,与分式$\frac{ax+ay}{{x}^{2}-{y}^{2}}$相等的是( )
| A. | $\frac{2a}{x+y}$ | B. | $\frac{a}{x+y}$ | C. | $\frac{2a}{x-y}$ | D. | $\frac{a}{x-y}$ |

 已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,且关于x的一元二次方程(b+c)x2-2ax-(b-c)=0有两个相等的实数根.
已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,且关于x的一元二次方程(b+c)x2-2ax-(b-c)=0有两个相等的实数根. 如图,由直径分别为4厘米、6厘米和10厘米的三个半圆所组成的图形,则图中阴影部分的面积为10π 平方厘米.
如图,由直径分别为4厘米、6厘米和10厘米的三个半圆所组成的图形,则图中阴影部分的面积为10π 平方厘米.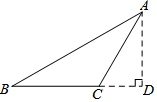 如图,在△ABC中,AB=17,BC=9,AC=10,试求△ABC的面积.
如图,在△ABC中,AB=17,BC=9,AC=10,试求△ABC的面积. 某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口$\frac{3}{2}$小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口$\frac{3}{2}$小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?