题目内容
16.先化简,再求值.$\frac{{a}^{2}-a}{{a}^{2}-2a+1}$+$\frac{2}{a-1}$-$\frac{1}{a}$,其中a=-1.分析 原式通分并利用同分母分式的加减法则计算得到最简结果,把a的值代入计算即可求出值.
解答 解:原式=$\frac{a(a-1)}{(a-1)^{2}}$+$\frac{2}{a-1}$-$\frac{1}{a}$=$\frac{a+2}{a-1}$-$\frac{1}{a}$=$\frac{{a}^{2}+2a-a+1}{a(a-1)}$=$\frac{{a}^{2}+a+1}{{a}^{2}-a}$,
当a=-1时,原式=$\frac{1}{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.下列语句正确的是( )
| A. | 弧所在的圆的半径越大,则弧越长 | |
| B. | 弧对应的圆心角越大,则弧越长 | |
| C. | 圆的半径扩大3倍,圆心角不变,则对应的扇形面积扩大3倍 | |
| D. | 圆的半径不变,圆心角扩大3倍,则对应的扇形面积扩大3倍 |
4.当实数m取任何值时,直线y=x+$\frac{3}{4}$m与直线y=-x-m2+2m-2的交点都不可能在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
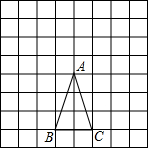 如图,在由完全相同的小正方形组成的网格中,△ABC的三个顶点都在格点上.
如图,在由完全相同的小正方形组成的网格中,△ABC的三个顶点都在格点上.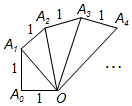 如图是由一系列直角三角形组成的螺旋形,OA0=A0A1=A1A2=…=1,则第n个直角三角形的面积为$\frac{\sqrt{n}}{2}$.
如图是由一系列直角三角形组成的螺旋形,OA0=A0A1=A1A2=…=1,则第n个直角三角形的面积为$\frac{\sqrt{n}}{2}$.
 如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-5,1),点B的坐标为(-2,1),点C的坐标为(-2,3).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-5,1),点B的坐标为(-2,1),点C的坐标为(-2,3).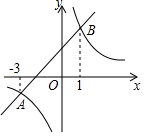 如图,双曲线y=$\frac{m}{x}$(m≠0)和直线y=x+b交于A,B两点,其横坐标分别为-3,1,则m的值是( )
如图,双曲线y=$\frac{m}{x}$(m≠0)和直线y=x+b交于A,B两点,其横坐标分别为-3,1,则m的值是( )