题目内容
17. 某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口$\frac{3}{2}$小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口$\frac{3}{2}$小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
分析 根据路程=速度×时间分别求得PQ、PR的长,再进一步根据勾股定理的逆定理可以证明三角形PQR是直角三角形,从而求解.
解答 解:根据题意,得
PQ=16×1.5=24(海里),
PR=12×1.5=18(海里),
QR=30(海里),
∵242+182=302,
即PQ2+PR2=QR2,
∴∠QPR=90°.
由“远洋号”沿东北方向航行可知,∠QPS=45°,则∠SPR=45°,
即“海天”号沿西北方向航行.
点评 本题考查路程、速度、时间之间的关系,勾股定理的逆定理、方位角等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
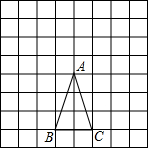 如图,在由完全相同的小正方形组成的网格中,△ABC的三个顶点都在格点上.
如图,在由完全相同的小正方形组成的网格中,△ABC的三个顶点都在格点上.
 如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-5,1),点B的坐标为(-2,1),点C的坐标为(-2,3).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-5,1),点B的坐标为(-2,1),点C的坐标为(-2,3).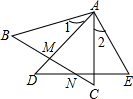 如图,△ABC和△ADE中,∠1=∠2,AB=AD,AC=AE,BC交AD于M,AC交DE于N,则图中全等三角形的对数有( )
如图,△ABC和△ADE中,∠1=∠2,AB=AD,AC=AE,BC交AD于M,AC交DE于N,则图中全等三角形的对数有( )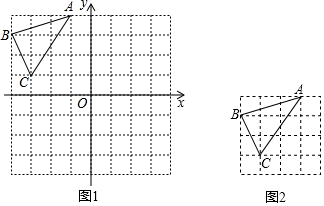
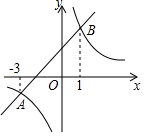 如图,双曲线y=$\frac{m}{x}$(m≠0)和直线y=x+b交于A,B两点,其横坐标分别为-3,1,则m的值是( )
如图,双曲线y=$\frac{m}{x}$(m≠0)和直线y=x+b交于A,B两点,其横坐标分别为-3,1,则m的值是( ) 如图,已知线段AB,BC,∠ABC=90°
如图,已知线段AB,BC,∠ABC=90°