题目内容
因式分解.
(1)-4x3+16x2-26x;
(2)
a2(x-2a)2-
a(2a-x)3;
(3)(x2+2x)2+2(x2+2x)+1;
(4)2x2+2x+
.
(1)-4x3+16x2-26x;
(2)
| 1 |
| 2 |
| 1 |
| 4 |
(3)(x2+2x)2+2(x2+2x)+1;
(4)2x2+2x+
| 1 |
| 2 |
考点:提公因式法与公式法的综合运用
专题:
分析:(1)直接提取公因式-2x,进而得出答案即可;
(2)首先提取公因式
a(2a-x)2,进而得出答案即可;
(3)直接利用完全平方公式分解因式进而得出答案;
(4)首先提取公因式2,进而利用完全平方公式分解因式即可.
(2)首先提取公因式
| 1 |
| 4 |
(3)直接利用完全平方公式分解因式进而得出答案;
(4)首先提取公因式2,进而利用完全平方公式分解因式即可.
解答:解:(1)-4x3+16x2-26x
=-2x(2x2-8x+13);
(2)
a2(x-2a)2-
a(2a-x)3
=
a(2a-x)2[2a-(2a-x)]
=
a(2a-x)2x;
(3)(x2+2x)2+2(x2+2x)+1
=(x2+2x+1)2
=(x+1)4;
(4)2x2+2x+
=2(x2+x+
)
=2(x+
)2.
=-2x(2x2-8x+13);
(2)
| 1 |
| 2 |
| 1 |
| 4 |
=
| 1 |
| 4 |
=
| 1 |
| 4 |
(3)(x2+2x)2+2(x2+2x)+1
=(x2+2x+1)2
=(x+1)4;
(4)2x2+2x+
| 1 |
| 2 |
=2(x2+x+
| 1 |
| 4 |
=2(x+
| 1 |
| 2 |
点评:此题主要考查了提取公因式法以及公式法分解因式,熟练掌握完全平方公式的形式是解题关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 若经过三角形某一个顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形的生成三角形,简称生成三角形.
若经过三角形某一个顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形的生成三角形,简称生成三角形.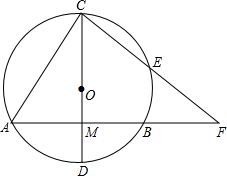 如图,⊙O的弦AB=8,直径CD⊥AB于M,OM:MD=3:2,E是劣弧CB上一点,连结CE并延长交CE的延长线于点F.求:
如图,⊙O的弦AB=8,直径CD⊥AB于M,OM:MD=3:2,E是劣弧CB上一点,连结CE并延长交CE的延长线于点F.求: 如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点在格点上.且A(1,-4),B(5,-4),C(4,-1)
如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点在格点上.且A(1,-4),B(5,-4),C(4,-1) 如图,?ABCD的对角线AC,BD交与点O.E,F分别是OA、OC的中点.
如图,?ABCD的对角线AC,BD交与点O.E,F分别是OA、OC的中点.