题目内容
实数m既能使关于x的不等式组
无解,又能使关于x的一元二次方程(m-1)x2-4x+1=0有两个不相等的实数根,则m的取值范围是 .
|
考点:根的判别式,解一元一次不等式组
专题:计算题
分析:根据不等式组的解法由不等式组
无解得到m≥-1,再根据判别式的意义得到m-1≠0且△=16-4(m-1)>0,解得m<5且m≠1,然后写出它们的公共部分即可得到m的取值范围.
|
解答:解:∵不等式组
无解,
∴x>m,x<-1,
则m≥-1,
∵一元二次方程(m-1)x2-4x+1=0有两个不相等的实数根,
∴m-1≠0且△=16-4(m-1)>0,解得m<5且m≠1,
∴m的取值范围为-1≤m<5且m≠1.
故答案为-1≤m<5且m≠1.
|
∴x>m,x<-1,
则m≥-1,
∵一元二次方程(m-1)x2-4x+1=0有两个不相等的实数根,
∴m-1≠0且△=16-4(m-1)>0,解得m<5且m≠1,
∴m的取值范围为-1≤m<5且m≠1.
故答案为-1≤m<5且m≠1.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了解一元一次不等式组.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
方程x(x-1)=2(x-1)的根为( )
| A、1 | B、2 | C、1和2 | D、-1和2 |
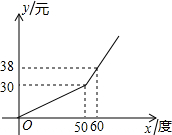 电力公司为增强人们节约用电意识,采取用户每月电量分段计费的方法收费,每月的电费y(元)与用电量x(度)之间的函数关系如图所示.若某用户二、三月的电费分别为39.6元和24元,则该用户三月份比二月份节约用电
电力公司为增强人们节约用电意识,采取用户每月电量分段计费的方法收费,每月的电费y(元)与用电量x(度)之间的函数关系如图所示.若某用户二、三月的电费分别为39.6元和24元,则该用户三月份比二月份节约用电 如图,AB∥CD,∠ABE=60°,∠F=50°,则∠E的度数为
如图,AB∥CD,∠ABE=60°,∠F=50°,则∠E的度数为