题目内容
 如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点在格点上.且A(1,-4),B(5,-4),C(4,-1)
如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点在格点上.且A(1,-4),B(5,-4),C(4,-1)(1)求出△ABC的面积;
(2)若把△ABC向上平移2个单位长度,再向左平移4个单位长度得到△A′B′C′,在图中画出△A′B′C′,并写出B′的坐标;
(3)求边AC在这一过程中所扫过的面积.
考点:作图-平移变换
专题:
分析:(1)根据三角形的面积等于矩形的面积减去三个顶点上三角形的面积即可得出结论;
(2)根据图形平移的性质画出△A′B′C′,并写出B′的坐标即可;
(3)根据边AC在这一过程中所扫过的面积是平行四边形即可得出结论.
(2)根据图形平移的性质画出△A′B′C′,并写出B′的坐标即可;
(3)根据边AC在这一过程中所扫过的面积是平行四边形即可得出结论.
解答: 解:(1)S△ABC=3×4-
解:(1)S△ABC=3×4-
×1×3-
×3×4
=12-
-6
=
;
(2)如图所示,B′(0,-2);
(3)S四边形=AA′C′C=8×5-
×2×5-
×3×3-
×2×5-
×3×3
=40-5-
-5-
=21.
 解:(1)S△ABC=3×4-
解:(1)S△ABC=3×4-| 1 |
| 2 |
| 1 |
| 2 |
=12-
| 3 |
| 2 |
=
| 9 |
| 2 |
(2)如图所示,B′(0,-2);
(3)S四边形=AA′C′C=8×5-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=40-5-
| 9 |
| 2 |
| 9 |
| 2 |
=21.
点评:本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
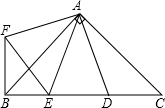 如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将
如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将 计算如图阴影部分面积:
计算如图阴影部分面积: 如图,菱形ABCD,四个顶点分别是A(-2,-1),B(1,-3),C(4,-1),D(1,1).将菱形沿y轴正方向平移3个单位长度,各个顶点的坐标变为多少?画出平移后的图形.
如图,菱形ABCD,四个顶点分别是A(-2,-1),B(1,-3),C(4,-1),D(1,1).将菱形沿y轴正方向平移3个单位长度,各个顶点的坐标变为多少?画出平移后的图形.