题目内容
 如图,?ABCD的对角线AC,BD交与点O.E,F分别是OA、OC的中点.
如图,?ABCD的对角线AC,BD交与点O.E,F分别是OA、OC的中点.求证:BE=DF.
考点:平行四边形的性质,全等三角形的判定与性质
专题:证明题
分析:由全等三角形的判定定理SAS证得△BEO≌△DFO,则该全等三角形的对应边相等:BE=DF.
解答:证明:如图,∵四边形ABCD是平行四边形,对角线AC、BD交于点O,
∴OB=OD,OA=OC.
又∵E,F分别是OA、OC的中点,
∴OE=
OA,OF=
OC,
∴OE=OF.
∵在△BEO与△DFO中,
,
∴△BEO≌△DFO(SAS),
∴BE=DF.
∴OB=OD,OA=OC.
又∵E,F分别是OA、OC的中点,
∴OE=
| 1 |
| 2 |
| 1 |
| 2 |
∴OE=OF.
∵在△BEO与△DFO中,
|
∴△BEO≌△DFO(SAS),
∴BE=DF.
点评:本题主要考查了全等三角形的判定与性质、平行四边形的性质的运用.
此题运用了平行四边形的对角线互相平分的性质和全等三角形对应边相等的性质.
此题运用了平行四边形的对角线互相平分的性质和全等三角形对应边相等的性质.

练习册系列答案
相关题目
 计算如图阴影部分面积:
计算如图阴影部分面积: 如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P、Q为AB边及BC边上的两个动点.
如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P、Q为AB边及BC边上的两个动点.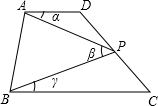 如图,已知四边形ABCD,AD∥BC.点P在直线CD上运动(点P和点C,D不重合,点P,A,B不在同一条直线上),若记∠DAP,∠APB,∠PBC分别为∠α,∠β,∠γ.
如图,已知四边形ABCD,AD∥BC.点P在直线CD上运动(点P和点C,D不重合,点P,A,B不在同一条直线上),若记∠DAP,∠APB,∠PBC分别为∠α,∠β,∠γ. 如图,菱形ABCD,四个顶点分别是A(-2,-1),B(1,-3),C(4,-1),D(1,1).将菱形沿y轴正方向平移3个单位长度,各个顶点的坐标变为多少?画出平移后的图形.
如图,菱形ABCD,四个顶点分别是A(-2,-1),B(1,-3),C(4,-1),D(1,1).将菱形沿y轴正方向平移3个单位长度,各个顶点的坐标变为多少?画出平移后的图形.