题目内容
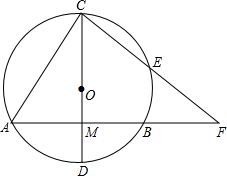 如图,⊙O的弦AB=8,直径CD⊥AB于M,OM:MD=3:2,E是劣弧CB上一点,连结CE并延长交CE的延长线于点F.求:
如图,⊙O的弦AB=8,直径CD⊥AB于M,OM:MD=3:2,E是劣弧CB上一点,连结CE并延长交CE的延长线于点F.求:(1)⊙O的半径;
(2)求CE•CF的值.
考点:垂径定理,勾股定理,相似三角形的判定与性质
专题:计算题
分析:(1)连结OB,设OM=3k,则MD=2k,OD=5k,根据垂径定理由直径CD⊥AB得到BM=AM=
AB=4,在Rt△OBM中,OB=5k,OM=3k,根据勾股定理得BM=4k,
则4k=4,解得k=1,于是得到圆O的半径为5;
(2)连结AE,如图,在Rt△ACM中,CM=OC+OM=8,AM=4,由勾股定理计算出AC2=AM2+CM2=80,根据垂径定理由直径CD⊥AB得到弧AC=弧BC,在根据圆周角定理得∠AEC=∠CAF,易证得△CAE∽△CFA,得到相似比AC:CF=CE:AC,然后根据比例性质得CE•CF=AC2=80.
| 1 |
| 2 |
则4k=4,解得k=1,于是得到圆O的半径为5;
(2)连结AE,如图,在Rt△ACM中,CM=OC+OM=8,AM=4,由勾股定理计算出AC2=AM2+CM2=80,根据垂径定理由直径CD⊥AB得到弧AC=弧BC,在根据圆周角定理得∠AEC=∠CAF,易证得△CAE∽△CFA,得到相似比AC:CF=CE:AC,然后根据比例性质得CE•CF=AC2=80.
解答:解: (1)连结OB,设OM=3k,则MD=2k,OD=5k,
(1)连结OB,设OM=3k,则MD=2k,OD=5k,
∵直径CD⊥AB,
∴BM=AM=
AB=4,
在Rt△OBM中,OB=5k,OM=3k,
∴BM=
=4k,
∴4k=4,解得k=1,
∴圆O的半径为5;
(2)连结AE,如图,
在Rt△ACM中,CM=OC+OM=5+3=8,AM=4,
∴AC2=AM2+CM2=16+64=80,
∵直径CD⊥AB,
∴弧AC=弧BC,
∴∠AEC=∠CAF,
又∵∠ACF=∠FCA,
∴△CAE∽△CFA,
∴AC:CF=CE:AC,
∴CE•CF=AC2=80.
 (1)连结OB,设OM=3k,则MD=2k,OD=5k,
(1)连结OB,设OM=3k,则MD=2k,OD=5k,∵直径CD⊥AB,
∴BM=AM=
| 1 |
| 2 |
在Rt△OBM中,OB=5k,OM=3k,
∴BM=
| OB2-OM2 |
∴4k=4,解得k=1,
∴圆O的半径为5;
(2)连结AE,如图,
在Rt△ACM中,CM=OC+OM=5+3=8,AM=4,
∴AC2=AM2+CM2=16+64=80,
∵直径CD⊥AB,
∴弧AC=弧BC,
∴∠AEC=∠CAF,
又∵∠ACF=∠FCA,
∴△CAE∽△CFA,
∴AC:CF=CE:AC,
∴CE•CF=AC2=80.
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理和相似三角形的判定与性质.

练习册系列答案
相关题目
 如图,AB∥CD,∠ABE=60°,∠F=50°,则∠E的度数为
如图,AB∥CD,∠ABE=60°,∠F=50°,则∠E的度数为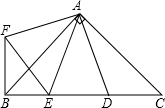 如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将
如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将 已知:如图,点A、B、C在一条直线上,AD∥BE,∠1=∠2.求证:∠A=∠E.
已知:如图,点A、B、C在一条直线上,AD∥BE,∠1=∠2.求证:∠A=∠E.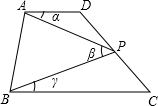 如图,已知四边形ABCD,AD∥BC.点P在直线CD上运动(点P和点C,D不重合,点P,A,B不在同一条直线上),若记∠DAP,∠APB,∠PBC分别为∠α,∠β,∠γ.
如图,已知四边形ABCD,AD∥BC.点P在直线CD上运动(点P和点C,D不重合,点P,A,B不在同一条直线上),若记∠DAP,∠APB,∠PBC分别为∠α,∠β,∠γ.