题目内容
12.(1)解分式方程:$\frac{2-x}{x-3}=\frac{1}{3-x}-2$(2)先化简,再求值:$\frac{{a}^{2}-2ab+{b}^{2}}{2a-b}$÷($\frac{1}{b}$-$\frac{1}{a}$),其中a=$\root{3}{-27}$,b=$\sqrt{16}$.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把a与b的值代入计算即可求出值.
解答 解:(1)方程两边同时乘以(x-3),得2-x=-1-2(x-3),
解得:x=3,
经检验:x=3是原分式方程的解;
(2)原式=$\frac{(a-b)^{2}}{2a-b}$÷$\frac{a-b}{ab}$=$\frac{(a-b)^{2}}{2a-b}$•$\frac{ab}{a-b}$=$\frac{ab(a-b)}{2a-b}$
当a=$\root{3}{-27}$=-3,b=$\sqrt{16}$=4时,原式=$\frac{-3×4×(-7)}{-6-4}$=8.4.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
 在△ABC中,∠A=120°,AB=12,AC=6.求tanB的值.
在△ABC中,∠A=120°,AB=12,AC=6.求tanB的值.
 如图,已知矩形ABCD∽矩形BCFE,AD=AE=1,则AB的长为$\frac{1+\sqrt{5}}{2}$.
如图,已知矩形ABCD∽矩形BCFE,AD=AE=1,则AB的长为$\frac{1+\sqrt{5}}{2}$.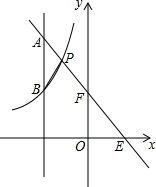 如图,直线l:y=-2x+2与双曲线y=$\frac{2k}{x}$(x<0)交于点P,只观察下图:
如图,直线l:y=-2x+2与双曲线y=$\frac{2k}{x}$(x<0)交于点P,只观察下图: