题目内容
2. 在△ABC中,∠A=120°,AB=12,AC=6.求tanB的值.
在△ABC中,∠A=120°,AB=12,AC=6.求tanB的值.
分析 过点C作CD⊥AB,根据∠A=120°,∠DAC=60°,由三角函数得出AD,CD,在Rt△BCD中,∠B的正切即可得出答案.
解答 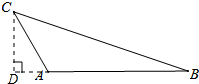 解:过点C作CD⊥AB,交BA的延长线于点D,
解:过点C作CD⊥AB,交BA的延长线于点D,
∴∠A=120°,
∴∠DAC=60°,
∴cos60°=$\frac{AD}{AC}$,sin60°=$\frac{CD}{AC}$,
∵AB=12,AC=6,
∴AD=AC•cos60°=6×$\frac{1}{2}$=3,
CD=AC•sin60°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
在Rt△BCD中,tanB=$\frac{CD}{BD}$=$\frac{3\sqrt{3}}{15}$=$\frac{\sqrt{3}}{5}$.
点评 本题考查了解直角三角形,解直角三角形的关键是把给出的这些三角形的条件放到直角三角形中,如果不是直角三角形就要通过添加辅助线来完成.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.如果x=-1,y=2,那么式子$\frac{(x-y)^{3}}{{x}^{3}-{y}^{3}}$的值是( )
| A. | 1 | B. | 3 | C. | $\frac{1}{9}$ | D. | $\frac{1}{7}$ |
17.已知⊙P的半径为2,点P的坐标为(2,1),点Q的坐标为(0,4),则点Q的位置( )
| A. | 在⊙P外 | B. | 在⊙P上 | C. | 在⊙P内 | D. | 不能确定 |
14.若二次函数y=(m+2)x2-3x+1与x轴有两个交点,则m的取值范围是( )
| A. | $m<\frac{1}{4}$ | B. | $m<-\frac{1}{4}且m≠-2$ | C. | $m<-\frac{1}{4}$ | D. | $m<\frac{1}{4}且m≠-2$ |