Question

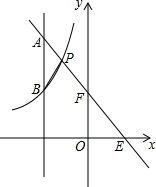
2．如图，直线l：y=-2x+2与双曲线y=$\frac{2k}{x}$（x＜0）交于点P，只观察下图：
（1）若交点P坐标为（-1，n），写出图中满足-2x+2＞$\frac{2k}{x}$的x取值范围；
（2）若交点P坐标为（x，4），若有一条平行于y轴的直线与直线l交于点A，与双曲线交于点B，其中A的横坐标为-2，求△ABP的面积．

Answer 1

分析 （1）根据图象直接可以得到答案．
（2）求出A、B、P三点坐标即可求出△ABP的面积．

解答 解：（1）由图象可知满足-2x+2＞$\frac{2k}{x}$的x的值为x＜-1．
（2）∵点P坐标为（x，4）在直线y=-2x+2上，
∴4=-2x+2，
∴x=-1，
∴点P（-1，4），
∴2k=-4，
∴k=-2，
∴双曲线为y=-$\frac{4}{x}$，
由题意A（-2，6），B（-2，2），
∴S_△ABP=$\frac{1}{2}$×4×1=2．

点评 本题考查函数的图象、三角形的面积计算，学会观察图象根据函数值的大小确定自变量的大小，能看懂图象信息是解题的关键．