题目内容
13.困式分解x4-4=(x2+2)(x+$\sqrt{2}$)(x-$\sqrt{2}$).(实数范围内分解).分析 先运用平方差公式,分解成(x2+2)(x2-2),再把x2-2写成x2-($\sqrt{2}$)2,符合平方差公式的特点,可以继续分解.
解答 解:x4-4=(x2+2)(x2-2)
=(x2+2)[x2-($\sqrt{2}$)2]=(x2+2)(x+$\sqrt{2}$)(x-$\sqrt{2}$).
故答案为:(x2+2)(x+$\sqrt{2}$)(x-$\sqrt{2}$).
点评 本题考查实数范围内的因式分解,因式分解的步骤为:一提公因式;二看公式.在实数范围内进行因式分解的式子的结果一般要分到出现无理数为止.

练习册系列答案
相关题目
4.代数式2016-a2+2ab-b2的最大值是( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 不存在 |
18.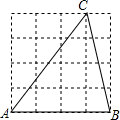 如图,在4的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,△ABC的顶点在格点上,则△ABC的三边长a,b,c的大小关系是( )
如图,在4的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,△ABC的顶点在格点上,则△ABC的三边长a,b,c的大小关系是( )
 如图,在4的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,△ABC的顶点在格点上,则△ABC的三边长a,b,c的大小关系是( )
如图,在4的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,△ABC的顶点在格点上,则△ABC的三边长a,b,c的大小关系是( )| A. | a<b<c | B. | c<b<a | C. | a<c<b | D. | c<a<b |
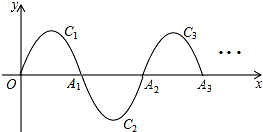 如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(35,m)在此“波浪线”上,则m的值为-2.
如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(35,m)在此“波浪线”上,则m的值为-2.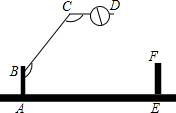 一个小区大门的栏杆如图所示,BA垂直地面AE于A,CD平行于地面AE,那么∠ABC+∠BCD=270度.
一个小区大门的栏杆如图所示,BA垂直地面AE于A,CD平行于地面AE,那么∠ABC+∠BCD=270度.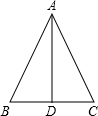 如图,在△ABC中,AB=AC=10cm,BC=12cm,AD⊥BC于点D,则AD=8cm.
如图,在△ABC中,AB=AC=10cm,BC=12cm,AD⊥BC于点D,则AD=8cm.