题目内容
1.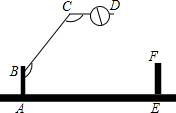 一个小区大门的栏杆如图所示,BA垂直地面AE于A,CD平行于地面AE,那么∠ABC+∠BCD=270度.
一个小区大门的栏杆如图所示,BA垂直地面AE于A,CD平行于地面AE,那么∠ABC+∠BCD=270度.
分析 作CH⊥AE于H,如图,根据平行线的性质得∠ABC+∠BCH=180°,∠DCH+∠CHE=180°,则∠DCH=90°,于是可得到∠ABC+∠BCD=270°.
解答 解:作CH⊥AE于H,如图,
∵AB⊥AE,CH⊥AE,
∴AB∥CH,
∴∠ABC+∠BCH=180°,
∵CD∥AE,
∴∠DCH+∠CHE=180°,
而∠CHE=90°,
∴∠DCH=90°,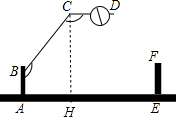
∴∠ABC+∠BCD=180°+90°=270°.
故答案为270.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
相关题目
11.下列命题中,真命题的是( )
| A. | 两个锐角的和为直角 | B. | 两个锐角的和为钝角 | ||
| C. | 两个锐角的和为锐角 | D. | 互余且非零度的两个角都是锐角 |
12.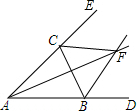 如图,△ABC外角∠CBD,∠BCE的平分线BF、CF相交于点F,则下列结论成立的是( )
如图,△ABC外角∠CBD,∠BCE的平分线BF、CF相交于点F,则下列结论成立的是( )
 如图,△ABC外角∠CBD,∠BCE的平分线BF、CF相交于点F,则下列结论成立的是( )
如图,△ABC外角∠CBD,∠BCE的平分线BF、CF相交于点F,则下列结论成立的是( )| A. | AF平分BC | B. | AF⊥BC | C. | AF平分∠BAC | D. | AF平分∠BFC |
10.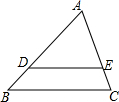 如图,在△ABC中,AB=4,AC=3,DE∥BC交AB于点D,交AC于点E,若AD=3,则AE的长为( )
如图,在△ABC中,AB=4,AC=3,DE∥BC交AB于点D,交AC于点E,若AD=3,则AE的长为( )
 如图,在△ABC中,AB=4,AC=3,DE∥BC交AB于点D,交AC于点E,若AD=3,则AE的长为( )
如图,在△ABC中,AB=4,AC=3,DE∥BC交AB于点D,交AC于点E,若AD=3,则AE的长为( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{9}{4}$ | D. | $\frac{4}{9}$ |
 如图所示,选择点O为对称中心,画出与△ABC关于点O对称的△A1B1C1.
如图所示,选择点O为对称中心,画出与△ABC关于点O对称的△A1B1C1.