抛物线y=2x2+4x+m与x轴的一个交点坐标为.则与x轴的另一个交点坐标为(1.0)．题目和参考答案——青夏教育精英家教网—

题目内容

2．抛物线y=2x²+4x+m与x轴的一个交点坐标为（-3，0），则与x轴的另一个交点坐标为（1，0）．

分析把交点坐标代入抛物线解析式求m的值，再令y=0解一元二次方程求另一交点的横坐标．

解答解：把点（-3，0）代入抛物线y=2x²+4x+m中，得m=-6，
所以，原方程为y=2x²+4x-6，
令y=0，解方程2x²+4x-6=0，得x₁=1，x₂=-3，
∴抛物线与x轴的另一个交点的坐标是（1，0）．
故答案为：（1，0）．

点评本题考查了点的坐标与抛物线解析式的关系，抛物线与x轴交点坐标的求法．本题也可以用根与系数关系直接求解．

练习册系列答案

相关题目

12．

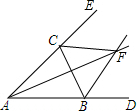如图，△ABC外角∠CBD，∠BCE的平分线BF、CF相交于点F，则下列结论成立的是（　　）

13．困式分解x⁴-4=（x²+2）（x+$\sqrt{2}$）（x-$\sqrt{2}$）．（实数范围内分解）．

10．

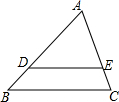如图，在△ABC中，AB=4，AC=3，DE∥BC交AB于点D，交AC于点E，若AD=3，则AE的长为（　　）

17．（1）解方程：$\frac{2}{{{x^{\;}}+3}}-\frac{x-3}{2x+6}=1$
（2）解不等式组：$\left\{\begin{array}{l}2x-1＞3（{x-1}）\\ \frac{5-x}{2}＜x+4.\end{array}\right.$．

7．将456 000 000用科学记数法表示为4.56×10⁸．

14．

已知一次函数y=kx+b的图象经过点（-1，-2），且与正比例函数y=$\frac{1}{2}$x的图象相交于点（2，a）．
（1）求a、b、k的值；
（2）在图中画出这两个函数图象，并求这两个函数图象与x轴所围成的三角形面积．

11．计算：
（1）$\frac{a^2}{a-1}-a-1$；
（2）$\frac{a-2}{a}÷\frac{{{a^2}-4}}{{{a^2}+a}}-1$．

12．一个多边形的内角和是900°，则它是（　　）边形．

试题分类