题目内容
8.在同一直角坐标系中,二次函数的图象与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3)一次函数的图象与抛物线交于B,C两点.(1)求二次函数的解析式;
(2)结合图象,直接写出当一次函数值小于二次函数值时自变量x的取值范围.
分析 (1)先根据题意,将A(-1,0)、点B(3,0)和点C(0,-3)代入二次函数的解析式,求得a、b、c的值,然后将其代入抛物线y=ax2+bx+c,从而求得二次函数的解析式;
(2)根据函数的图象,一次函数值小于二次函数值,即对于相同的x的值,一次函数对应的图象在下边,即可直接写出x的范围.
解答 解:(1)根据题意,知$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=-3}\end{array}\right.$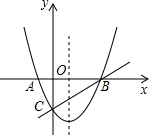 ,
,
解得,$\left\{\begin{array}{l}{a=}\\{b=-2}\\{c=-3}\end{array}\right.$,
故二次函数的表达式是:y=x2-2x-3;
(2)根据图象可得一次函数值小于二次函数值时自变量x的取值范围上x<0或x>3.
点评 本题考查了待定系数法求函数的解析式,以及二次函数的性质,正确根据函数的图象比较函数值的大小是关键.

练习册系列答案
相关题目
3.将二次函数y=x2+1的图象向右平移1个单位,则平移后的二次函数的解析式为( )
| A. | y=x2 | B. | y=(x-1)2 | C. | y=(x-1)2+1 | D. | y=(x+1)2+1 |
18.如图,从边长为(a+1)cm的正方形纸片中剪去一个边长为(a-1)cm的正方形(a>1),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则该矩形的面积是( )
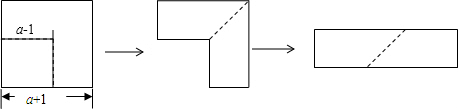

| A. | 2 cm2 | B. | 2a cm2 | C. | 4a cm2 | D. | (a2-1)cm2 |
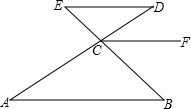 如图:已知∠A=∠D,∠B=∠FCB,能否确定ED与CF的位置关系,
如图:已知∠A=∠D,∠B=∠FCB,能否确定ED与CF的位置关系, 如图所示,选择点O为对称中心,画出与△ABC关于点O对称的△A1B1C1.
如图所示,选择点O为对称中心,画出与△ABC关于点O对称的△A1B1C1.