题目内容
18．
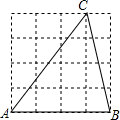如图，在4的正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫做格点，△ABC的顶点在格点上，则△ABC的三边长a，b，c的大小关系是（ ）| A． | a＜b＜c | B． | c＜b＜a | C． | a＜c＜b | D． | c＜a＜b |
分析 首先利用勾股定理求出a，b，c的长，再比较大小即可．
解答 解：
由勾股定理可得：a=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$，b=$\sqrt{{4}^{2}+{3}^{2}}$=5，
∵c=4，
∴c＜a＜b，
故选D．
点评 本题考查了勾股定理的运用以及比较实数的大小，熟记勾股定理是解题的关键．
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
10．
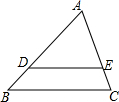如图，在△ABC中，AB=4，AC=3，DE∥BC交AB于点D，交AC于点E，若AD=3，则AE的长为（ ）
如图，在△ABC中，AB=4，AC=3，DE∥BC交AB于点D，交AC于点E，若AD=3，则AE的长为（ ）| A． | $\frac{4}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{9}{4}$ | D． | $\frac{4}{9}$ |
如图，一架5米长的梯子AB，斜靠在一堵竖直的墙AO上，这时梯顶A距地面4米，若梯子沿墙下滑1米，则梯足B外滑1米．