题目内容
1. 如图,四边形ABCD中,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.
如图,四边形ABCD中,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.(1)求证:AE平分∠BAD;
(2)判断AB、CD、AD之间的数量关系,并证明;
(3)若AD=10,CB=8,求S△ADE.
分析 (1)过点E作EF⊥DA于点F,首先根据角的平分线上的点到角的两边的距离相等可得CE=EF,根据等量代换可得BE=EF,再根据角平分线的判定可得AE平分∠BAD;
(2)首先证明Rt△DFE和Rt△DCE可得DC=DF,同理可得AF=AB,再由AD=AF+DF利用等量代换可得结论;
(3)根据角平分线的性质可得EF=CE,再利用三角形的面积公式可得答案.
解答 (1)证明:过点E作EF⊥DA于点F,
∵∠C=90°,DE平分∠ADC,
∴CE=EF,
∵E是BC的中点,
∴BE=CE,
∴BE=EF,
又∵∠B=90°,EF⊥AD,
∴AE平分∠BAD.
(2)证明:AD=CD+AD,
∵∠C=∠DFE=90°,
∴在Rt△DFE和Rt△DCE中$\left\{\begin{array}{l}{DE=DE}\\{EF=CE}\end{array}\right.$,
∴Rt△DFE和Rt△DCE(HL),
∴DC=DF,
同理AF=AB,
∵AD=AF+DF,
∴AD=CD+AD;
(3)解:∵CB=8,E是BC的中点,
∴CE=4,
∴EF=4,
∵AD=10,
∴S△ADE=10×4×$\frac{1}{2}$=20.
点评 此题主要考查了角平分线的性质和判定,以及全等三角形的性质和判定,关键是掌握角平分线的性质和判定定理.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
16.三角形中,若一个角等于其他两个角的和,则这个三角形是( )
| A. | 钝角三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 等腰三角形 |
 在△ABC中,AD是高,E是AD的中点,连接CE,并延长交AB于点P,过点A作AQ∥BC,交CP的延长线于点Q,BD:CD:AD=1:2:3.
在△ABC中,AD是高,E是AD的中点,连接CE,并延长交AB于点P,过点A作AQ∥BC,交CP的延长线于点Q,BD:CD:AD=1:2:3.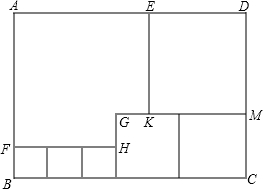 如图所示,用三种大小不同的六个正方形和一个缺角的长方形拼成长方形ABCD,其中,GH=2cm,GK=2cm,设BF=x cm,
如图所示,用三种大小不同的六个正方形和一个缺角的长方形拼成长方形ABCD,其中,GH=2cm,GK=2cm,设BF=x cm,